
Core (graph theory)
Encyclopedia
In the mathematical
field of graph theory
, a core is a notion that describes behavior of a graph
with respect to graph homomorphism
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a core is a notion that describes behavior of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with respect to graph homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
s.
Definition
- Graph
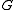 is a core if every homomorphism
is a core if every homomorphism 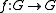 is an isomorphismGraph isomorphismIn graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
is an isomorphismGraph isomorphismIn graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
, that is it is a bijection of vertices of .
. - A core of a graph
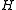 is a graph
is a graph  such that
such that
- There exists a homomorphism from
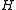 to
to 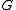 ,
, - there exists a homomorphism from
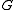 to
to 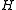 , and
, and -
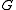 is minimal with this property.
is minimal with this property.
Examples
- Any complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
is a core. - A cycleCycle (graph theory)In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
of odd length is a core. - A core of a cycle of even length is
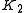 .
.
Properties
- Core of a graph is determined uniquely, up to isomorphismGraph isomorphismIn graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
. - If
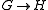 and
and 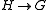 then the graphs
then the graphs 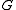 and
and 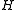 have isomorphic cores.
have isomorphic cores.
See also
- the k-coreDegeneracy (graph theory)In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
of a graph, obtained by iteratively removing all vertices of degree at most k, is a different notion.

