In knot theory

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

, Conway notation, invented by John Horton Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

, is a way of describing knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

s that makes many of their properties clear. It composes a knot

Knot

A knot is a method of fastening or securing linear material such as rope by tying or interweaving. It may consist of a length of one or several segments of rope, string, webbing, twine, strap, or even chain interwoven such that the line can bind to itself or to some other object—the "load"...

 using certain operations on tangles to construct it.

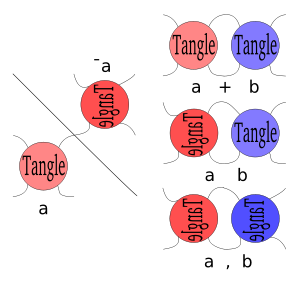
Tangles

In Conway notation, the tangles are generally algebraic 2-tangles. This means their tangle diagrams consist of 2 arcs and 4 points on the edge of the diagram; furthermore, they are built up from rational tangles using the Conway operations.

[The following seems to be attempting to describe only integer or 1/n rational tangles]
Tangles consisting only of positive crossings are denoted by the number of crossings, or if there are only negative crossings it is denoted by a negative number. If the arcs are not crossed, or can be transformed to into an uncrossed position with the Reidemeister moves, it is called the 0 or ∞ tangle, depending on the orientation of the tangle.

Operations on tangles

If a tangle, a, is reflected on the NW-SE line, it is denoted by ^-a. (Note that this is different than a tangle with a negative number of crossings.)Tangles have three binary operation

Binary operation

In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....

s, sum, product, and ramification, however all can be explained using tangle addition and negation. The tangle product, a b, is equivalent to ^-a+b. and ramification or a,b, is equivalent to ^-a+^-b.

Advanced concepts

Rational tangles are equivalent if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

their fractions are equal. An accessible proof of this fact is given in (Kauffman and Lambropoulou 2004). A number before an asterisk, *, denotes the polyhedron number; multiple asterisks indicate that multiple polyhedra of that number exist.