
Confidence band
Encyclopedia
A confidence band is used in statistical analysis
to represent the uncertainty in an estimate of a curve or function based on limited or noisy data. Confidence bands are often used as part of the graphical presentation of results in a statistical analysis. Confidence bands are closely related to confidence intervals, which represent the uncertainty in an estimate of a single numerical value.
In mathematical terms, a pointwise confidence band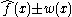 with coverage probability 1−α satisfies the following condition separately for each value of x:
with coverage probability 1−α satisfies the following condition separately for each value of x:
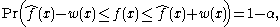
where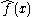 is the point estimate of f(x).
is the point estimate of f(x).
The simultaneous coverage probability of a collection of confidence intervals is the probability that all of them cover their corresponding true values simultaneously. In the example above, the simultaneous coverage probability is the probability that the intervals for x=18,19,... all cover their true values (assuming that 18 is the youngest age at which a person can vote). If each interval individually has coverage probability 0.95, the simultaneous coverage probability is generally less than 0.95. A 95% simultaneous confidence band is a collection of confidence intervals for all values x in the domain of f(x) that is constructed to have simultaneous coverage probability 0.95.
In mathematical terms, a simultaneous confidence band with coverage probability 1−α satisfies the following condition:
with coverage probability 1−α satisfies the following condition:
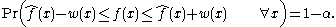
In nearly all cases, a simultaneous confidence band will be wider than a pointwise confidence band with the same coverage probability.
. In the case of a simple regression involving a single independent variable, results can be presented in the form of a plot showing the estimated regression line along with either point-wise or simultaneous confidence bands. Commonly used methods for constructing simultaneous confidence bands in regression are the Bonferroni and Scheffé
methods.
For example, confidence bands can be constructed around estimates of the empirical distribution function
. Simple theory allows the construction of point-wise confidence intervals, but it is also possible to construct a simultaneous confidence band for the cumulative distribution function as a whole by inverting the Kolmogorov-Smirnov test, or by using non-parametric likelihood methods
.
Confidence bands have also been devised for estimates of density functions
, spectral density
functions
, quantile
functions, scatterplot smooths
, survival function
s, and characteristic functions
.
s in the same way that confidence bands are related to confidence intervals. Prediction bands commonly arise in regression analysis. The goal of a prediction band is to cover with a prescribed probability the values of one or more future observations from the same population from which a given data set was sampled. Just as prediction intervals are wider than confidence intervals, prediction bands will be wider than confidence bands.
In mathematical terms, a prediction band with coverage probability 1−α satisfies the following condition for each value of x:
with coverage probability 1−α satisfies the following condition for each value of x:
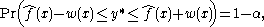
where y* is an observation taken from the data-generating process at the given point x that is independent of the data used to construct the point estimate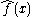 and the confidence interval w(x). This is a pointwise prediction interval. It would be possible to construct a simultaneous interval for a finite number of independent observations using, for example, the Bonferroni method to widen the interval by an appropriate amount.
and the confidence interval w(x). This is a pointwise prediction interval. It would be possible to construct a simultaneous interval for a finite number of independent observations using, for example, the Bonferroni method to widen the interval by an appropriate amount.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
to represent the uncertainty in an estimate of a curve or function based on limited or noisy data. Confidence bands are often used as part of the graphical presentation of results in a statistical analysis. Confidence bands are closely related to confidence intervals, which represent the uncertainty in an estimate of a single numerical value.
Pointwise and simultaneous confidence bands
Suppose our aim is to estimate a function f(x). For example, f(x) might be the proportion of people of a particular age x who support a given candidate in an election. If x is measured at the precision of a single year, we can construct a separate 95% confidence interval for each age. Each of these confidence intervals covers the corresponding true value f(x) with probability 0.95. Taken together, these confidence intervals constitute a 95% pointwise confidence band for f(x).In mathematical terms, a pointwise confidence band
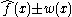 with coverage probability 1−α satisfies the following condition separately for each value of x:
with coverage probability 1−α satisfies the following condition separately for each value of x: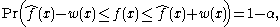
where
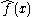 is the point estimate of f(x).
is the point estimate of f(x).The simultaneous coverage probability of a collection of confidence intervals is the probability that all of them cover their corresponding true values simultaneously. In the example above, the simultaneous coverage probability is the probability that the intervals for x=18,19,... all cover their true values (assuming that 18 is the youngest age at which a person can vote). If each interval individually has coverage probability 0.95, the simultaneous coverage probability is generally less than 0.95. A 95% simultaneous confidence band is a collection of confidence intervals for all values x in the domain of f(x) that is constructed to have simultaneous coverage probability 0.95.
In mathematical terms, a simultaneous confidence band
 with coverage probability 1−α satisfies the following condition:
with coverage probability 1−α satisfies the following condition: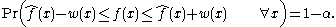
In nearly all cases, a simultaneous confidence band will be wider than a pointwise confidence band with the same coverage probability.
Confidence bands in regression analysis
Confidence bands commonly arise in regression analysisRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
. In the case of a simple regression involving a single independent variable, results can be presented in the form of a plot showing the estimated regression line along with either point-wise or simultaneous confidence bands. Commonly used methods for constructing simultaneous confidence bands in regression are the Bonferroni and Scheffé
Scheffé's method
In statistics, Scheffé's method, named after Henry Scheffé, is a method for adjusting significance levels in a linear regression analysis to account for multiple comparisons...
methods.
Other applications of confidence bands
Confidence bands arise whenever a statistical analysis focuses on estimating a function.For example, confidence bands can be constructed around estimates of the empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
. Simple theory allows the construction of point-wise confidence intervals, but it is also possible to construct a simultaneous confidence band for the cumulative distribution function as a whole by inverting the Kolmogorov-Smirnov test, or by using non-parametric likelihood methods
.
Confidence bands have also been devised for estimates of density functions
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
functions
, quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
functions, scatterplot smooths
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. Many different algorithms are used in smoothing...
, survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
s, and characteristic functions
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
.
Prediction bands
Prediction bands are related to prediction intervalPrediction interval
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which future observations will fall, with a certain probability, given what has already been observed...
s in the same way that confidence bands are related to confidence intervals. Prediction bands commonly arise in regression analysis. The goal of a prediction band is to cover with a prescribed probability the values of one or more future observations from the same population from which a given data set was sampled. Just as prediction intervals are wider than confidence intervals, prediction bands will be wider than confidence bands.
In mathematical terms, a prediction band
 with coverage probability 1−α satisfies the following condition for each value of x:
with coverage probability 1−α satisfies the following condition for each value of x: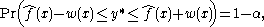
where y* is an observation taken from the data-generating process at the given point x that is independent of the data used to construct the point estimate
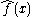 and the confidence interval w(x). This is a pointwise prediction interval. It would be possible to construct a simultaneous interval for a finite number of independent observations using, for example, the Bonferroni method to widen the interval by an appropriate amount.
and the confidence interval w(x). This is a pointwise prediction interval. It would be possible to construct a simultaneous interval for a finite number of independent observations using, for example, the Bonferroni method to widen the interval by an appropriate amount.

