Conductivity near the percolation threshold
Encyclopedia
In a mixture between a dielectric and a metallic component, the conductivity
and the dielectric constant
of this mixture show a critical behavior if the fraction of the metallic component reaches the percolation threshold
. The behavior of the conductivity near this percolation threshold will show a smooth changeover from the conductivity of the dielectric component to the conductivity of the metallic component and can be described using two critical exponents
s and t, whereas the dielectric constant will diverge if the threshold is approached from either side. To include the frequency
dependent behavior, a resistor
-capacitor
model (R-C model) is used.
On a regular lattice, the bond between two nearest neighbors can either be occupied with probability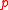
or not occupied with probability 
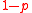. It exists a critical value 
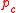. For occupation probabilities 
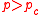an infinite cluster of the occupied bonds is formed. This value 
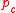is called the percolation threshold. The region near to this percolation threshold can be described by the two critical exponents 
and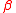 
(see Percolation critical exponents).
With this critical exponents we have the correlation length,
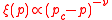
and the percolation probability, P:
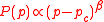
. And the dielectric component with conductivity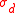 
corresponds to non-occupied bonds. We consider the two following well-known cases of a conductor-insulator mixture and a superconductor–conductor mixture.
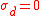. This case describes the behaviour, if the percolation threshold is approached from above:
for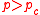
Below the percolation threshold we have no conductivity, because of the perfect insulator and just finite metallic clusters. The exponent t is one of the two critical exponents for electrical percolation.
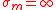. This case is useful for the description below the percolation threshold:
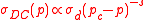
for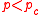
Now, above the percolation threshold the conductivity becomes infinite, because of the infinite superconducting clusters. And also we get the second critical exponent s for the electrical percolation.
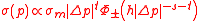
with
and 
At the percolation threshold, the conductivity reaches the value:
with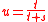
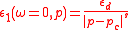
for the occupied bonds and by perfect capacitors with conductivity 
(where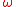 
represents the angular frequency
) for the non-occupied bonds. Now the scaling law takes the form:
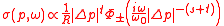
This scaling law contains a purely imaginary scaling variable and a critical time scale
which diverges if the percolation threshold is approached from above as well as from below.
Electrical resistivity and conductivity
Electrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
and the dielectric constantDielectric constant
The relative permittivity of a material under given conditions reflects the extent to which it concentrates electrostatic lines of flux. In technical terms, it is the ratio of the amount of electrical energy stored in a material by an applied voltage, relative to that stored in a vacuum...
of this mixture show a critical behavior if the fraction of the metallic component reaches the percolation thresholdPercolation threshold
Percolation threshold is a mathematical term related to percolation theory, which is the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist while above it, there exists a giant component of the order of system size...
. The behavior of the conductivity near this percolation threshold will show a smooth changeover from the conductivity of the dielectric component to the conductivity of the metallic component and can be described using two critical exponents
Critical exponent
Critical exponents describe the behaviour of physical quantities near continuous phase transitions. It is believed, though not proven, that they are universal, i.e...
s and t, whereas the dielectric constant will diverge if the threshold is approached from either side. To include the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
dependent behavior, a resistor
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
-capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
model (R-C model) is used.
Geometrical percolation
For describing such a mixture of a dielectric and a metallic component we use the model of bond-percolation.On a regular lattice, the bond between two nearest neighbors can either be occupied with probability
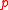or not occupied with probability 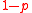. It exists a critical value 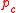. For occupation probabilities 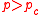an infinite cluster of the occupied bonds is formed. This value 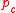is called the percolation threshold. The region near to this percolation threshold can be described by the two critical exponents and 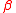(see Percolation critical exponents).With this critical exponents we have the correlation length,
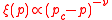
and the percolation probability, P:
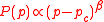
Electrical percolation
For the description of the electrical percolation, we identify the occupied bonds of the bond-percolation model with the metallic component having a conductivity. And the dielectric component with conductivity 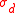corresponds to non-occupied bonds. We consider the two following well-known cases of a conductor-insulator mixture and a superconductor–conductor mixture.conductor-insulator mixture
In the case of a conductor-insulator mixture we have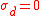. This case describes the behaviour, if the percolation threshold is approached from above:for
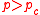
Below the percolation threshold we have no conductivity, because of the perfect insulator and just finite metallic clusters. The exponent t is one of the two critical exponents for electrical percolation.
superconductor–conductor mixture
In the other well-known case of a superconductor-conductor mixture we have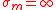. This case is useful for the description below the percolation threshold: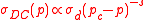for
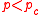
Now, above the percolation threshold the conductivity becomes infinite, because of the infinite superconducting clusters. And also we get the second critical exponent s for the electrical percolation.
conductivity near the percolation threshold
In the region around the percolation threshold, the conductivity assumes a scaling form: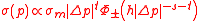with
and At the percolation threshold, the conductivity reaches the value:
with
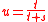
Values for the critical exponents
In different sources there exists some different values for the critical exponents s, t and u in 3 dimensions:| Efros et al. | Clerc et al. | Bergman et al. | |
|---|---|---|---|
| t | 1,60 | 1,90 | 2,00 |
| s | 1,00 | 0,73 | 0,76 |
| u | 0,62 | 0,72 | 0,72 |
Dielectric constant
The dielectric constant also shows a critical behavior near the percolation threshold. For the real part of the dielectric constant we have: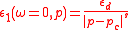The R-C model
Within the R-C model, the bonds in the percolation model are represented by pure resistors with conductivity for the occupied bonds and by perfect capacitors with conductivity (where represents the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
) for the non-occupied bonds. Now the scaling law takes the form:
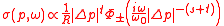
This scaling law contains a purely imaginary scaling variable and a critical time scale
which diverges if the percolation threshold is approached from above as well as from below.