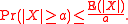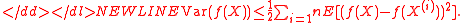Concentration inequality
Encyclopedia
In mathematics
, concentration inequalities provide probability bounds on how a random variable
deviates from some value (e.g. its expectation
). The laws of large numbers of classical probability theory state that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean
. Recent results shows that such behavior is shared by other functions of independent random variables.
Proof can be found here
.
We can extend Markov's inequality to a strictly increasing and non-negative function . We have
. We have
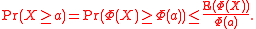
is a special case of generalized Markov's inequality when
If X is any random variable and a > 0, then

Where Var(X) is the variance of X, defined as:
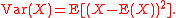
 and
and 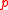 . The probability of getting exact
. The probability of getting exact  successes in
successes in  trials is given by the probability mass function
trials is given by the probability mass function
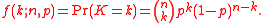
Let and
and 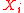 's are i.i.d. Bernoulli random variables with parameter
's are i.i.d. Bernoulli random variables with parameter 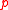 .
.  follows the binomial distribution with parameter with parameter
follows the binomial distribution with parameter with parameter  and
and 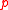 . Central Limit Theorem suggests when
. Central Limit Theorem suggests when  ,
, 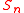 is approximately normally distributed with mean
is approximately normally distributed with mean 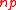 and variance
and variance 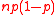 , and
, and
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, concentration inequalities provide probability bounds on how a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
deviates from some value (e.g. its expectation
Expectation
In the case of uncertainty, expectation is what is considered the most likely to happen. An expectation, which is a belief that is centered on the future, may or may not be realistic. A less advantageous result gives rise to the emotion of disappointment. If something happens that is not at all...
). The laws of large numbers of classical probability theory state that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
. Recent results shows that such behavior is shared by other functions of independent random variables.
Markov's inequality
If X is any random variable and a > 0, thenProof can be found here
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
.
We can extend Markov's inequality to a strictly increasing and non-negative function
 . We have
. We have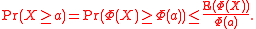
Chebyshev's inequality
Chebyshev's inequalityChebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
is a special case of generalized Markov's inequality when

If X is any random variable and a > 0, then

Where Var(X) is the variance of X, defined as:
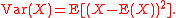
Asymptotic behavior of binomial distribution
If a random variable X follows the binomial distribution with parameter and
and 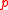 . The probability of getting exact
. The probability of getting exact  successes in
successes in  trials is given by the probability mass function
trials is given by the probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
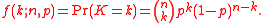
Let
 and
and 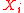 's are i.i.d. Bernoulli random variables with parameter
's are i.i.d. Bernoulli random variables with parameter 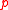 .
.  follows the binomial distribution with parameter with parameter
follows the binomial distribution with parameter with parameter  and
and 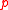 . Central Limit Theorem suggests when
. Central Limit Theorem suggests when  ,
, 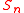 is approximately normally distributed with mean
is approximately normally distributed with mean 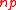 and variance
and variance 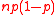 , and
, and-

For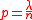 , where
, where  is a constant, the limit distribution of binomial distribution
is a constant, the limit distribution of binomial distribution 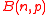 is the Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
is the Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
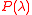
General Chernoff inequality
A Chernoff boundChernoff boundIn probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
gives exponentially decreasing bounds on tail distributions of sums of independent random variables. Let denote independent but not necessarily identical random variables, satisfying
denote independent but not necessarily identical random variables, satisfying  , for
, for 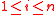 .
.
we have lower tail inequality:
-

If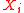 satisfies
satisfies  , we have upper tail inequality:
, we have upper tail inequality:
-
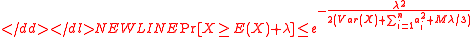
If are i.i.d.,
are i.i.d., 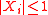 and
and 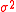 is the variance of
is the variance of  . A typical version of Chernoff Inequality is:
. A typical version of Chernoff Inequality is:
-

Hoeffding's inequality
Hoeffding's inequalityHoeffding's inequalityIn probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
can be stated as follows:
If : are independent. Assume that the
are independent. Assume that the 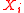 are almost surely bounded; that is, assume for
are almost surely bounded; that is, assume for 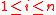 that
that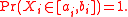
Then, for the empirical mean of these variables

we have the inequalities (Hoeffding 1963, Theorem 2 ):
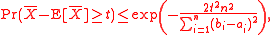
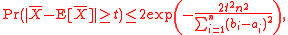
Bennett's inequality
Bennett's inequalityBennett's inequalityIn probability theory, Bennett's inequality provides an upper bound on the probability that the sum of independent random variables deviates from its expected value by more than any specified amount...
was proved by George Bennett of the University of New South WalesUniversity of New South WalesThe University of New South Wales , is a research-focused university based in Kensington, a suburb in Sydney, New South Wales, Australia...
in 1962.
Let
be independent random variables, and assume (for simplicity but without loss of generalityWithout loss of generalityWithout loss of generality is a frequently used expression in mathematics...
) they all have zero expected value. Further assume almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
for all , and let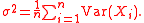
Then for any ,
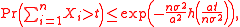
where .
Bernstein's inequality
Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive ,
,

Efron–Stein nequality
The Efron–Stein inequality (or influence inequality, or MG bound on variance) bounds the variance of a general function.
Suppose that ,
,  are independent with
are independent with 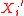 and
and 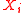 having the same distribution for all
having the same distribution for all  .
.
Let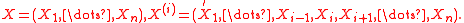 Then
Then
-
-
-
-