Completely randomized design
Encyclopedia
In the design of experiments
, completely randomized designs are for studying the effects of one primary factor without the need to take other nuisance variable
s into account. This article describes completely randomized designs that have one primary factor. The experiment compares the values of a response variable based on the different levels of that primary factor. For completely randomized designs, the levels of the primary factor are randomly assigned
to the experimental units.
, that is to say the run sequence of the experimental units is determined randomly. For example, if there are 3 levels of the primary factor with each level to be run 2 times, then there are 6! (where ! denotes factorial
) possible run sequences (or ways to order the experimental trials). Because of the replication
, the number of unique orderings is 90 (since 90 = 6!/(2!*2!*2!)). An example of an unrandomized design would be to always run 2 replications for the first level, then 2 for the second level, and finally 2 for the third level. To randomize the runs, one way would be to put 6 slips of paper in a box with 2 having level 1, 2 having level 2, and 2 having level 3. Before each run, one of the slips would be drawn blindly from the box and the level selected would be used for the next run of the experiment.
In practice, the randomization is typically performed by a computer program. However, the randomization can also be generated from random number table
s or by some physical mechanism (e.g., drawing the slips of paper).
and the total sample size
(number of runs) is N = k × L × n. Balance dictates that the number of replications be the same at each level of the factor (this will maximize the sensitivity of subsequent statistical t- (or F-) tests).
Note that in this example there are 12!/(3!*3!*3!*3!) = 369,600 ways to run the experiment, all equally likely to be picked by a randomization procedure.
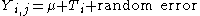
with
with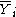
= average of all Y for which X1 = i.
Statistical tests for levels of X1 are those used for a one-way ANOVA
and are detailed in the article on analysis of variance
.
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, completely randomized designs are for studying the effects of one primary factor without the need to take other nuisance variable
Nuisance variable
In statistics, a nuisance parameter is any parameter which is not of immediate interest but which must be accounted for in the analysis of those parameters which are of interest...
s into account. This article describes completely randomized designs that have one primary factor. The experiment compares the values of a response variable based on the different levels of that primary factor. For completely randomized designs, the levels of the primary factor are randomly assigned
Random assignment
Random assignment or random placement is an experimental technique for assigning subjects to different treatments . The thinking behind random assignment is that by randomizing treatment assignment, then the group attributes for the different treatments will be roughly equivalent and therefore any...
to the experimental units.
Randomization
By randomizationRandomization
Randomization is the process of making something random; this means:* Generating a random permutation of a sequence .* Selecting a random sample of a population ....
, that is to say the run sequence of the experimental units is determined randomly. For example, if there are 3 levels of the primary factor with each level to be run 2 times, then there are 6! (where ! denotes factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
) possible run sequences (or ways to order the experimental trials). Because of the replication
Replication (statistics)
In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "the repetition of the set of all the treatment combinations to be compared in...
, the number of unique orderings is 90 (since 90 = 6!/(2!*2!*2!)). An example of an unrandomized design would be to always run 2 replications for the first level, then 2 for the second level, and finally 2 for the third level. To randomize the runs, one way would be to put 6 slips of paper in a box with 2 having level 1, 2 having level 2, and 2 having level 3. Before each run, one of the slips would be drawn blindly from the box and the level selected would be used for the next run of the experiment.
In practice, the randomization is typically performed by a computer program. However, the randomization can also be generated from random number table
Random number table
Random number tables have been used in statistics for tasks such as selected random samples. This was much more effective than manually selecting the random samples...
s or by some physical mechanism (e.g., drawing the slips of paper).
Three key numbers
All completely randomized designs with one primary factor are defined by 3 numbers:- k = number of factors (= 1 for these designs)
- L = number of levels
- n = number of replications
and the total sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
(number of runs) is N = k × L × n. Balance dictates that the number of replications be the same at each level of the factor (this will maximize the sensitivity of subsequent statistical t- (or F-) tests).
Example
A typical example of a completely randomized design is the following:- k = 1 factor (X1)
- L = 4 levels of that single factor (called "1", "2", "3", and "4")
- n = 3 replications per level
- N = 4 levels × 3 replications per level = 12 runs
Sample randomized sequence of trials
The randomized sequence of trials might look like: X1: 3, 1, 4, 2, 2, 1, 3, 4, 1, 2, 4, 3Note that in this example there are 12!/(3!*3!*3!*3!) = 369,600 ways to run the experiment, all equally likely to be picked by a randomization procedure.
Model for a completely randomized design
The model for the response is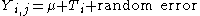with
- Yi,j being any observation for which X1 = i (i and j denote the level of the factor and the replication within the level of the factor, respectively)
- μ (or mu) is the general location parameterLocation parameterIn statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
- Ti is the effect of having treatment level i
Estimating and testing model factor levels
- Estimate for μ :
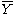= the averageAverageIn mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
of all the data - Estimate for Ti :
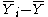
with
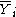= average of all Y for which X1 = i.Statistical tests for levels of X1 are those used for a one-way ANOVA
One-way ANOVA
In statistics, one-way analysis of variance is a technique used to compare means of two or more samples . This technique can be used only for numerical data....
and are detailed in the article on analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
.