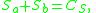Complementary sequences
Encyclopedia
In applied mathematics, complementary sequences (CS) are pairs of sequence
s with the useful property that their out-of-phase aperiodic autocorrelation
coefficients sum to zero. Binary complementary sequences were first introduced by Marcel J. E. Golay
in 1949. In 1961–1962 Golay gave several methods for constructing sequences of length 2N and gave examples of complementary sequences of lengths 10 and 26. In 1974 R. J. Turyn gave a method for constructing sequences of length mn from sequences of lengths m and n which allows the construction of sequences of any length of the form 2N10K26M.
Later the theory of complementary sequences was generalized by other authors to polyphase complementary sequences, multilevel complementary sequences, and arbitrary complex complementary sequences. Complementary sets have also been considered; these can contain more than two sequences.
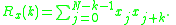
Then the pair of sequences a and b is complementary if:

for k = 1, ..., N − 1.
Or using Kronecker delta we can write:

where C is a constant.
So we can say that the sum of autocorrelation functions of complementary sequences is a delta function which is an ideal autocorrelations for many applications like radar
pulse compression
and spread spectrum
telecommunications.
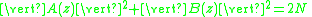
for all z on the unit circle, that is, |z| = 1. If so, A and B form a Golay pair of polynomials. Examples include the Shapiro polynomials
, which give rise to complementary sequences of length a power of 2.
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s with the useful property that their out-of-phase aperiodic autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
coefficients sum to zero. Binary complementary sequences were first introduced by Marcel J. E. Golay
Marcel J. E. Golay
Marcel J.E. Golay was a Swiss-born mathematician, physicist, and information theorist, who applied mathematics to real-world military and industrial problems. He was born in Neuchâtel, Switzerland.-Career:...
in 1949. In 1961–1962 Golay gave several methods for constructing sequences of length 2N and gave examples of complementary sequences of lengths 10 and 26. In 1974 R. J. Turyn gave a method for constructing sequences of length mn from sequences of lengths m and n which allows the construction of sequences of any length of the form 2N10K26M.
Later the theory of complementary sequences was generalized by other authors to polyphase complementary sequences, multilevel complementary sequences, and arbitrary complex complementary sequences. Complementary sets have also been considered; these can contain more than two sequences.
Definition
Let (a0, a1, ..., aN − 1) and (b0, b1, ..., bN − 1) be a pair of bipolar sequences, meaning that a(k) and b(k) have values +1 or −1. Let the aperiodic autocorrelation function of the sequence x be defined by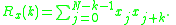
Then the pair of sequences a and b is complementary if:

for k = 1, ..., N − 1.
Or using Kronecker delta we can write:

where C is a constant.
So we can say that the sum of autocorrelation functions of complementary sequences is a delta function which is an ideal autocorrelations for many applications like radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
pulse compression
Pulse compression
Pulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio...
and spread spectrum
Spread spectrum
Spread-spectrum techniques are methods by which a signal generated in a particular bandwidth is deliberately spread in the frequency domain, resulting in a signal with a wider bandwidth...
telecommunications.
Examples
- As the simplest example we have sequences of length 2: (+1, +1) and (+1, −1). Their autocorrelation functions are (2, 1) and (2, −1), which add up to (4, 0).
- As the next example (sequences of length 4), we have (+1, +1, +1, −1) and (+1, +1, −1, +1). Their autocorrelation functions are (4, 1, 0, −1) and (4, −1, 0, 1), which add up to (8, 0, 0, 0).
- One example of length 8 is (+1, +1, +1, −1, +1, +1, −1, +1) and (+1, +1, +1, −1, −1, −1, +1, −1). Their autocorrelation functions are (8, −1, 0, 3, 0, 1, 0, 1) and (8, 1, 0, −3, 0, −1, 0, −1).
- An example of length 10 given by Golay is (+1, +1, −1, +1, −1, +1, −1, −1, +1, +1) and (+1, +1, −1, +1, +1, +1, +1, +1, −1, −1). Their autocorrelation functions are (10, 1, 2, 3, −2, −1, 0, −1, 0, 1) and (10, −1, −2, −3, 2, 1, 0, 1, 0, −1).
Properties of complementary pairs of sequences
- Complementary sequencesSéquencesSéquences is a French-language film magazine originally published in Montreal, Quebec by the Commission des ciné-clubs du Centre catholique du cinéma de Montréal, a Roman Catholic film society. Founded in 1955, the publication was edited for forty years by Léo Bonneville, a member of the Clerics...
have complementary spectra. As the autocorrelation function and the power spectra form a Fourier pair complementary sequences also have complementary spectra. But as the Fourier transform of a delta function is a constant we can write
- where CS is a constant.
- Sa and Sb are defined as a squared magnitude of the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the sequences. The Fourier transform can be a direct DFT of the sequences, it can be a DFT of zero padded sequences or it can be a continuous Fourier transform of the sequences which is equivalent to the Z transform for Z = ejω.
- CS spectra is upper bounded. As Sa and Sb are non-negative values we can write
- also
- If any of the sequences of the CS pair is inverted (multiplied by −1) they remain complementary. More generally if any of the sequences is multiplied by ejφ they remain complementary;
- If any of the sequences is reverted (inverted in time) they remain complemantary;
- If any of the sequences is delayed they remain complementary;
- If the sequences are interchanged they remain complementary;
- If both sequences are multiplied by the same constant (real or complex) they remain complementary;
- If both sequences are decimated in time by K they remain complementary. More precisely if from a complementary pair ((a(k), b(k)) we form a new pair (a(Nk), b(N*k)) with zero samples in between then the new sequences are complementary.
- If alternating bits of both sequences are inverted they remain complementary. In general for arbitrary complex sequences if both sequences are multiplied by ejπkn/N (where k is a constant and n is the time index) they remain complementary
- A new pair of complementary sequences can be formed as [a b] and [a −b] where [..] denotes concatenation and a and b are a pair of CS;
- A new pair of sequences can be formed as {a b} and {a −b} where {..} denotes interleaving of sequences.
- A new pair of sequences can be formed as a + b and a − b.
Golay pair
A complementary pair a, b may be encoded as polynomials A(z) = a(0) + a(1)z + ... + a(N − 1)zN−1 and similarly for B(z). The complementarity property of the sequences is equivalent to the condition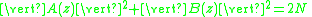
for all z on the unit circle, that is, |z| = 1. If so, A and B form a Golay pair of polynomials. Examples include the Shapiro polynomials
Shapiro polynomials
In mathematics, the Shapiro polynomials are a sequence of polynomials which were first studied by Harold S. Shapiro in 1951 when considering the magnitude of specific trigonometric sums. In signal processing, the Shapiro polynomials have good autocorrelation properties and their values on the unit...
, which give rise to complementary sequences of length a power of 2.
Applications of complementary sequences
- Multislit spectrometry
- Ultrasound measurements
- Acoustic measurements
- radarRadarRadar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
pulse compressionPulse compressionPulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio... - Wi-FiWi-FiWi-Fi or Wifi, is a mechanism for wirelessly connecting electronic devices. A device enabled with Wi-Fi, such as a personal computer, video game console, smartphone, or digital audio player, can connect to the Internet via a wireless network access point. An access point has a range of about 20...
networks, - 3G3G3G or 3rd generation mobile telecommunications is a generation of standards for mobile phones and mobile telecommunication services fulfilling the International Mobile Telecommunications-2000 specifications by the International Telecommunication Union...
CDMA wireless networks - OFDM communication systems
- Train wheel detection systems
- Non-destructive tests (NDT)
- Communications
See also
- Pseudorandom binary sequences (also called maximum length sequenceMaximum length sequenceA maximum length sequence is a type of pseudorandom binary sequence.They are bit sequences generated using maximal linear feedback shift registers and are so called because they are periodic and reproduce every binary sequence that can be reproduced by the shift registers...
s or M-sequences) - Gold sequencesGold codeA Gold code, also known as Gold sequence, is a type of binary sequence, used in telecommunication and satellite navigation . Gold codes are named after Robert Gold. Gold codes have bounded small cross-correlations within a set, which is useful when multiple devices are broadcasting in the same range...
- Kasami sequencesKasami codeKasami sequences are binary sequences of length 2N-1 where N is an even integer. Kasami sequences have good cross-correlation values approaching the Welch lower bound. There are two classes of Kasami sequences - the small set and the large set....
- Walsh–Hadamard sequencesWalsh matrixIn mathematics, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product of any two distinct rows is zero. The Walsh matrix was proposed by Joseph Leonard Walsh in 1923...
- Binary Golay codeBinary Golay codeIn mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
(Error-correcting code) - Ternary Golay codeTernary Golay codeThere are two closely related error-correcting codes known as ternary Golay codes. The code generally known simply as the ternary Golay code is a perfect [11, 6, 5] ternary linear code; the extended ternary Golay code is a [12, 6, 6] linear code obtained by adding a zero-sum check digit to the...
(Error-correcting code)