
Combined gas law
Encyclopedia
The combined gas law is a gas law which combines Charles's law
, Boyle's law
, and Gay-Lussac's law
. These laws each relate one thermodynamic variable
to another mathematically while holding everything else constant. Charles's law states that volume and temperature are directly proportional to each other as long as pressure is held constant. Boyle's law asserts that pressure and volume are inversely proportional to each other at fixed temperature. Finally, Gay-Lussac's law introduces a direct proportionality between temperature and pressure as long as it is at a constant volume. The inter-dependence of these variables is shown in the combined gas law, which clearly states that:
This can be stated mathematically as
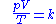
where:
For comparing the same substance under two different sets of conditions, the law can be written as:
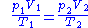
The addition of Avogadro's law
to the combined gas law yields the ideal gas law
.
states that the pressure-volume product is constant: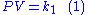
Charles's Law
shows that the volume is proportional to absolute temperature: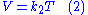
Gay-Lussac's Law
says that the pressure is proportional to the absolute temperature: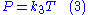
where P is the pressure
, V the volume and T the absolute temperature and of an ideal gas
.
By combining (1) and either of (2) or (3) we can gain a new equation with P, V and T. Equation (2) is used in this example, and the arbitrary subscript on the constant is dropped so that k = k2.
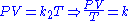
Substituting in Avogadro's Law
yields the ideal gas equation.
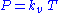 ............(1) Gay-Lussac's Law, volume assumed constant
............(1) Gay-Lussac's Law, volume assumed constant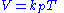 ............(2) Charles's Law, pressure assumed constant
............(2) Charles's Law, pressure assumed constant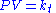 ............(3) Boyle's Law, temperature assumed constant
............(3) Boyle's Law, temperature assumed constant
where kv, kp, and kt are the constants, one can multiply the three together to obtain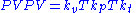
Taking the square root of both sides and dividing by T appears to produce of the desired result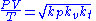
However, if before applying the above procedure, one merely rearranges the terms in Boyle's Law, kt = P V, then after canceling and rearranging, one obtains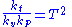
which is not very helpful if not misleading.
A physical derivation, longer but more reliable, begins by realizing that the constant volume parameter in Gay-Lussac's law will change as the system volume changes. At constant volume V1 the law might appear P = k1 T while at constant volume V2 it might appear P= k2 T .
Denoting this "variable constant volume" by kv(V), rewrite the law as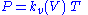 ............(4)
............(4)
The same consideration applies to the constant in Charles's law which may rewritten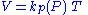 ............(5)
............(5)
In seeking to find kv(V), one should not unthinkingly eliminate T between (4) and (5) since P is varying in the former while it is assumed constant in the latter. Rather it should first be determined in what sense these equations are compatible with one another. To gain insight into this, recall that any two variables determine the third. Choosing P and V to be independent we picture the T values forming a surface above the PV plane. A definite V0 and P0 define a T0, a point on that surface. Substituting these values in (4) and (5), and rearranging yields
Since these both describe what is happening at the same point on the surface the two numeric expressions can be equated and rearranged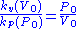 ............(6)
............(6)
The kv(V0) and kp(P0)are the slopes of orthogonal lines through that surface point. Their ratio depends only on P0 / V0 at that point.
Note that the functional form of (6) did not depend on the particular point chosen. The same formula would have arisen for any other combination of P and V values. Therefore one can write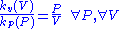 ............(7)
............(7)
This says each point on the surface has it own pair of orthogonal lines through it, with their slope ratio depending only on that point. Whereas (6) is a relation between specific slopes and variable values, (7) is a relation between slope functions and function variables. It holds true for any point on the surface, i.e. for any and all combinations of P and V values. To solve this equation for the function kv(V) first separate the variables, V on the left and P on the right.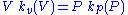
Choose any pressure P1. the right side evaluates to some arbitrary value, call it karb.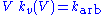 ............(8)
............(8)
This particular equation must now hold true, not just for one value of V but for all values of V. The only definition of kv(V) that guarantees this for all V and arbitrary karb is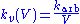 ............(9)
............(9)
which may be verified by substitution in (8).
Finally substituting (9) in Gay-Lussac's law (4) and rearranging produces the combined gas law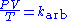
Note that Boyle's law was not used in this derivation but is easily deduced from the result. Generally any two of the three starting laws are all that is needed in this type of derivation - all starting pairs lead to the same combined gas law.
Charles's law
Charles' law is an experimental gas law which describes how gases tend to expand when heated. It was first published by French natural philosopher Joseph Louis Gay-Lussac in 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles...
, Boyle's law
Boyle's law
Boyle's law is one of many gas laws and a special case of the ideal gas law. Boyle's law describes the inversely proportional relationship between the absolute pressure and volume of a gas, if the temperature is kept constant within a closed system...
, and Gay-Lussac's law
Gay-Lussac's law
The expression Gay-Lussac's law is used for each of the two relationships named after the French chemist Joseph Louis Gay-Lussac and which concern the properties of gases, though it is more usually applied to his law of combining volumes, the first listed here...
. These laws each relate one thermodynamic variable
Conjugate variables (thermodynamics)
In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature/entropy or pressure/volume. In fact all thermodynamic potentials are expressed in terms of conjugate pairs....
to another mathematically while holding everything else constant. Charles's law states that volume and temperature are directly proportional to each other as long as pressure is held constant. Boyle's law asserts that pressure and volume are inversely proportional to each other at fixed temperature. Finally, Gay-Lussac's law introduces a direct proportionality between temperature and pressure as long as it is at a constant volume. The inter-dependence of these variables is shown in the combined gas law, which clearly states that:
This can be stated mathematically as
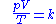
where:
- p is the pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
- V is the volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
- T is the temperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
measured in kelvinKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s - k is a constant (with units of energy divided by temperature).
For comparing the same substance under two different sets of conditions, the law can be written as:
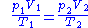
The addition of Avogadro's law
Avogadro's law
Avogadro's law is a gas law named after Amedeo Avogadro who, in 1811, hypothesized that two given samples of an ideal gas, at the same temperature, pressure and volume, contain the same number of molecules...
to the combined gas law yields the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
.
Derivation from the Gas Laws
Boyle's LawBoyle's law
Boyle's law is one of many gas laws and a special case of the ideal gas law. Boyle's law describes the inversely proportional relationship between the absolute pressure and volume of a gas, if the temperature is kept constant within a closed system...
states that the pressure-volume product is constant:
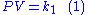
Charles's Law
Charles's law
Charles' law is an experimental gas law which describes how gases tend to expand when heated. It was first published by French natural philosopher Joseph Louis Gay-Lussac in 1802, although he credited the discovery to unpublished work from the 1780s by Jacques Charles...
shows that the volume is proportional to absolute temperature:
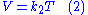
Gay-Lussac's Law
Gay-Lussac's law
The expression Gay-Lussac's law is used for each of the two relationships named after the French chemist Joseph Louis Gay-Lussac and which concern the properties of gases, though it is more usually applied to his law of combining volumes, the first listed here...
says that the pressure is proportional to the absolute temperature:
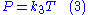
where P is the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, V the volume and T the absolute temperature and of an ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
.
By combining (1) and either of (2) or (3) we can gain a new equation with P, V and T. Equation (2) is used in this example, and the arbitrary subscript on the constant is dropped so that k = k2.
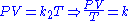
Substituting in Avogadro's Law
Avogadro's law
Avogadro's law is a gas law named after Amedeo Avogadro who, in 1811, hypothesized that two given samples of an ideal gas, at the same temperature, pressure and volume, contain the same number of molecules...
yields the ideal gas equation.
Physical Derivation
A derivation of the combined gas law using only elementary algebra can contain surprises. For example, starting from the three empirical laws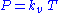 ............(1) Gay-Lussac's Law, volume assumed constant
............(1) Gay-Lussac's Law, volume assumed constant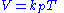 ............(2) Charles's Law, pressure assumed constant
............(2) Charles's Law, pressure assumed constant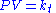 ............(3) Boyle's Law, temperature assumed constant
............(3) Boyle's Law, temperature assumed constantwhere kv, kp, and kt are the constants, one can multiply the three together to obtain
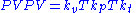
Taking the square root of both sides and dividing by T appears to produce of the desired result
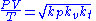
However, if before applying the above procedure, one merely rearranges the terms in Boyle's Law, kt = P V, then after canceling and rearranging, one obtains
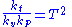
which is not very helpful if not misleading.
A physical derivation, longer but more reliable, begins by realizing that the constant volume parameter in Gay-Lussac's law will change as the system volume changes. At constant volume V1 the law might appear P = k1 T while at constant volume V2 it might appear P= k2 T .
Denoting this "variable constant volume" by kv(V), rewrite the law as
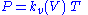 ............(4)
............(4)The same consideration applies to the constant in Charles's law which may rewritten
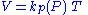 ............(5)
............(5)In seeking to find kv(V), one should not unthinkingly eliminate T between (4) and (5) since P is varying in the former while it is assumed constant in the latter. Rather it should first be determined in what sense these equations are compatible with one another. To gain insight into this, recall that any two variables determine the third. Choosing P and V to be independent we picture the T values forming a surface above the PV plane. A definite V0 and P0 define a T0, a point on that surface. Substituting these values in (4) and (5), and rearranging yields

Since these both describe what is happening at the same point on the surface the two numeric expressions can be equated and rearranged
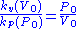 ............(6)
............(6)The kv(V0) and kp(P0)are the slopes of orthogonal lines through that surface point. Their ratio depends only on P0 / V0 at that point.
Note that the functional form of (6) did not depend on the particular point chosen. The same formula would have arisen for any other combination of P and V values. Therefore one can write
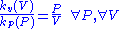 ............(7)
............(7)This says each point on the surface has it own pair of orthogonal lines through it, with their slope ratio depending only on that point. Whereas (6) is a relation between specific slopes and variable values, (7) is a relation between slope functions and function variables. It holds true for any point on the surface, i.e. for any and all combinations of P and V values. To solve this equation for the function kv(V) first separate the variables, V on the left and P on the right.
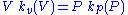
Choose any pressure P1. the right side evaluates to some arbitrary value, call it karb.
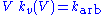 ............(8)
............(8)This particular equation must now hold true, not just for one value of V but for all values of V. The only definition of kv(V) that guarantees this for all V and arbitrary karb is
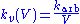 ............(9)
............(9)which may be verified by substitution in (8).
Finally substituting (9) in Gay-Lussac's law (4) and rearranging produces the combined gas law
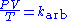
Note that Boyle's law was not used in this derivation but is easily deduced from the result. Generally any two of the three starting laws are all that is needed in this type of derivation - all starting pairs lead to the same combined gas law.
Applications
The combined gas law can be used to explain the mechanics where pressure, temperature, and volume are affected. For example: air conditioners, refrigerators and the formation of clouds.External links
- Interactive Java applet on the combined gas law by Wolfgang Bauer

