Conjugate variables (thermodynamics)
Encyclopedia
In thermodynamics
, the internal energy
of a system is expressed in terms of pairs of conjugate variables such as temperature/entropy or pressure/volume. In fact all thermodynamic potentials
are expressed in terms of conjugate pairs.
For a mechanical system, a small increment of energy is the product of a force times a small displacement. A similar situation exists in thermodynamics. An increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" which, when imbalanced, cause certain generalized "displacements"
, and the product of the two is the energy transferred as a result. These forces and their associated displacements are called conjugate variables. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy transfer. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, while all other extensive variables are held constant.
The thermodynamic square
can be used as a tool to recall and derive some of the thermodynamic potentials
based on conjugate variables.
The theory of thermodynamic potentials is not complete until we consider the number of particles in a system as a variable on par with the other extensive quantities such as volume and entropy. The number of particles is, like volume and entropy, the displacement variable in a conjugate pair. The generalized force component of this pair is the chemical potential
. The chemical potential may be thought of as a force which, when imbalanced, pushes an exchange of particles, either with the surroundings, or between phases inside the system. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds liquid water and water vapor, there will be a chemical potential (which is negative) for the liquid which pushes the water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate, and the chemical potentials of each phase is equal, is equilibrium obtained.
The most commonly considered conjugate thermodynamic variables are (with corresponding SI
units):
For a system with different types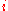
of particles, a small change in the internal energy is given by:
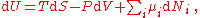
where U is internal energy, T is temperature, S is entropy, P is pressure, V is volume,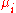
is the chemical potential of the i-th particle type, and 
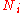is the number of i-type particles in the system.
Here, the temperature, pressure, and chemical potential are the generalized forces, which drive the generalized changes in entropy, volume, and particle number respectively. These parameters all affect the internal energy
of a thermodynamic system. A small change
in the internal energy of the system is given by the sum of the flow of energy across the boundaries of the system due to the corresponding conjugate pair. These concepts will be expanded upon in the following sections.
While dealing with processes in which systems exchange matter or energy, classical thermodynamics is not concerned with the rate
at which such processes take place, termed kinetics
. For this reason, the term thermodynamics is usually used synonymously with equilibrium thermodynamics. A central notion for this connection is that of quasistatic process
es, namely idealized, "infinitely slow" processes. Time-dependent thermodynamic processes far away from equilibrium are studied by non-equilibrium thermodynamics
. This can be done through linear or non-linear analysis of irreversible processes, allowing systems near and far away from equilibrium to be studied, respectively.
acts as a generalized force - pressure differences force a change in volume, and their product is the energy lost by the system due to mechanical work
. Pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables.
The above holds true only for non-viscous fluids. In the case of viscous fluids
, plastic
and elastic
solids, the pressure force is generalized to the stress tensor
, and changes in volume are generalized to the volume multiplied by the strain tensor . These then form a conjugate pair. If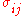
is the ij component of the stress tensor, and 
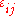is the ij component of the strain tensor, then the mechanical work done as the result of a stress-induced infinitesimal strain 
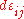is:
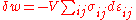
or, using Einstein notation
for the tensors, in which repeated indices are assumed to be summed:
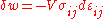
In the case of pure compression (i.e. no shearing forces), the stress tensor is simply the negative of the pressure times the unit tensor so that
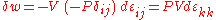
The trace
of the strain tensor (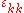
) is just the fractional change in volume so that the above reduces to 
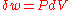as it should.
differences drive changes in entropy
, and their product is the energy transferred by heat
ing. We should note that this is the only heat term, the other terms are essentially all various forms of work.
is like a force which pushes an increase in particle number
. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds water and water vapor, there will be a chemical potential (which is negative) for the liquid pushing water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate is equilibrium obtained.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of a system is expressed in terms of pairs of conjugate variables such as temperature/entropy or pressure/volume. In fact all thermodynamic potentials
Thermodynamic potentials
A thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
are expressed in terms of conjugate pairs.
For a mechanical system, a small increment of energy is the product of a force times a small displacement. A similar situation exists in thermodynamics. An increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" which, when imbalanced, cause certain generalized "displacements"
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
, and the product of the two is the energy transferred as a result. These forces and their associated displacements are called conjugate variables. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy transfer. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, while all other extensive variables are held constant.
The thermodynamic square
Thermodynamic square
The thermodynamic square is a mnemonic diagram used to help determine thermodynamic relations. The corners represent common conjugate variables while the sides represent thermodynamic potentials...
can be used as a tool to recall and derive some of the thermodynamic potentials
Thermodynamic potentials
A thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
based on conjugate variables.
Overview
Just as a small increment of energy in a mechanical system is the product of a force times a small displacement, so an increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" which, when unbalanced, cause certain generalized "displacements" to occur, with their product being the energy transferred as a result. These forces and their associated displacements are called conjugate variables. For example, consider the pV conjugate pair. The pressure P acts as a generalized force: Pressure differences force a change in volume dV, and their product is the energy lost by the system due to work. Here pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables. In a similar way, temperature differences drive changes in entropy, and their product is the energy transferred by heat transfer. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy. The intensive (force) variable is the derivative of the (extensive) internal energy with respect to the extensive (displacement) variable, with all other extensive variables held constant.The theory of thermodynamic potentials is not complete until we consider the number of particles in a system as a variable on par with the other extensive quantities such as volume and entropy. The number of particles is, like volume and entropy, the displacement variable in a conjugate pair. The generalized force component of this pair is the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. The chemical potential may be thought of as a force which, when imbalanced, pushes an exchange of particles, either with the surroundings, or between phases inside the system. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds liquid water and water vapor, there will be a chemical potential (which is negative) for the liquid which pushes the water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate, and the chemical potentials of each phase is equal, is equilibrium obtained.
The most commonly considered conjugate thermodynamic variables are (with corresponding SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units):
- Thermal parameters:
- TemperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
: T (KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
) - EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
: S (J K-1)
- Temperature
- Mechanical parameters:
- PressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
: P (PaPascal (unit)The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
= J m-3) - Volume: V (m3 = J Pa-1)
- Pressure
-
- or, more generally,
- StressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
:
(PaPascal (unit)The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
= J m-3) - Volume × Strain:
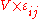(m3 = J Pa-1)
- Material parameters:
- chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
: μ (J) - particle numberParticle numberThe particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
: N (particles or mole)
- chemical potential
For a system with different types
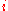of particles, a small change in the internal energy is given by: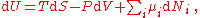where U is internal energy, T is temperature, S is entropy, P is pressure, V is volume,
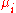is the chemical potential of the i-th particle type, and 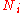is the number of i-type particles in the system.Here, the temperature, pressure, and chemical potential are the generalized forces, which drive the generalized changes in entropy, volume, and particle number respectively. These parameters all affect the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of a thermodynamic system. A small change
in the internal energy of the system is given by the sum of the flow of energy across the boundaries of the system due to the corresponding conjugate pair. These concepts will be expanded upon in the following sections.While dealing with processes in which systems exchange matter or energy, classical thermodynamics is not concerned with the rate
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
at which such processes take place, termed kinetics
Kinetics (physics)
In physics and engineering, kinetics is a term for the branch of classical mechanics that is concerned with the relationship between the motion of bodies and its causes, namely forces and torques...
. For this reason, the term thermodynamics is usually used synonymously with equilibrium thermodynamics. A central notion for this connection is that of quasistatic process
Quasistatic process
In thermodynamics, a quasistatic process is a thermodynamic process that happens infinitely slowly. However, it is very important of note that no real process is quasistatic...
es, namely idealized, "infinitely slow" processes. Time-dependent thermodynamic processes far away from equilibrium are studied by non-equilibrium thermodynamics
Non-equilibrium thermodynamics
Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium; for they are changing or can be triggered to change over time, and are continuously and discontinuously...
. This can be done through linear or non-linear analysis of irreversible processes, allowing systems near and far away from equilibrium to be studied, respectively.
The pressure/volume and stress/strain pair
As an example, consider the PV conjugate pair. The pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
acts as a generalized force - pressure differences force a change in volume, and their product is the energy lost by the system due to mechanical work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
. Pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables.
The above holds true only for non-viscous fluids. In the case of viscous fluids
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, plastic
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
and elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
solids, the pressure force is generalized to the stress tensor
Stress tensor
Stress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
, and changes in volume are generalized to the volume multiplied by the strain tensor . These then form a conjugate pair. If
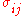is the ij component of the stress tensor, and 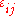is the ij component of the strain tensor, then the mechanical work done as the result of a stress-induced infinitesimal strain 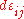is: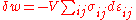or, using Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
for the tensors, in which repeated indices are assumed to be summed:
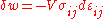
In the case of pure compression (i.e. no shearing forces), the stress tensor is simply the negative of the pressure times the unit tensor so that
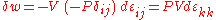
The trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the strain tensor (
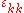) is just the fractional change in volume so that the above reduces to 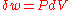as it should.The temperature/entropy pair
In a similar way, temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
differences drive changes in entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, and their product is the energy transferred by heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
ing. We should note that this is the only heat term, the other terms are essentially all various forms of work.
The chemical potential/particle number pair
The chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
is like a force which pushes an increase in particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example if a container holds water and water vapor, there will be a chemical potential (which is negative) for the liquid pushing water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate is equilibrium obtained.