
Collision problem
Encyclopedia
The r-to-1 collision problem is an important theoretical problem in complexity theory
, quantum computing, and computational mathematics
. The collision problem most often refers to the 2-to-1 version : given even and a function
even and a function 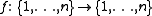 , we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of
, we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of 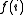 for any
for any 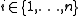 . The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.
. The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.
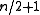 queries, and in general distinguishing r-to-1 functions from 1-to-1 functions requires
queries, and in general distinguishing r-to-1 functions from 1-to-1 functions requires 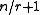 queries.
queries.
This is a straightforward application of the pigeonhole principle: if a function is r-to-1, then after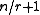 queries we are guaranteed to have found a collision. If a function is 1-to-1, then no collision exists. Thus,
queries we are guaranteed to have found a collision. If a function is 1-to-1, then no collision exists. Thus, 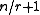 queries suffice. If we are unlucky, then the first
queries suffice. If we are unlucky, then the first 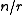 queries could return distinct answers, so
queries could return distinct answers, so 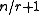 queries is also necessary.
queries is also necessary.
If we allow randomness, the problem is easier. By the birthday paradox
, if we choose (distinct) queries at random, then with high probability we find a collision in any fixed 2-to-1 function after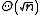 queries.
queries.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, quantum computing, and computational mathematics
Computational mathematics
Computational mathematics involves mathematical research in areas of science where computing plays a central and essential role, emphasizing algorithms, numerical methods, and symbolic methods. Computation in the research is prominent. Computational mathematics emerged as a distinct part of applied...
. The collision problem most often refers to the 2-to-1 version : given
 even and a function
even and a function 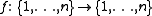 , we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of
, we are promised that f is either 1-to-1 or 2-to-1. We are only allowed to make queries about the value of 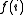 for any
for any 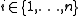 . The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.
. The problem then asks how many such queries we need to make to determine with certainty whether f is 1-to-1 or 2-to-1.Classical Solution
Solving the 2-to-1 version deterministically requires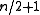 queries, and in general distinguishing r-to-1 functions from 1-to-1 functions requires
queries, and in general distinguishing r-to-1 functions from 1-to-1 functions requires 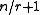 queries.
queries.This is a straightforward application of the pigeonhole principle: if a function is r-to-1, then after
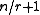 queries we are guaranteed to have found a collision. If a function is 1-to-1, then no collision exists. Thus,
queries we are guaranteed to have found a collision. If a function is 1-to-1, then no collision exists. Thus, 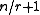 queries suffice. If we are unlucky, then the first
queries suffice. If we are unlucky, then the first 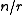 queries could return distinct answers, so
queries could return distinct answers, so 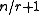 queries is also necessary.
queries is also necessary.If we allow randomness, the problem is easier. By the birthday paradox
Birthday paradox
In probability theory, the birthday problem or birthday paradox pertains to the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99%...
, if we choose (distinct) queries at random, then with high probability we find a collision in any fixed 2-to-1 function after
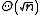 queries.
queries.

