
Club set
Encyclopedia
In mathematics
, particularly in mathematical logic
and set theory
, a club set is a subset of a limit ordinal which is closed
under the order topology
, and is unbounded relative to the limit ordinal. The name club is a contraction of closed and unbounded.
 is a limit ordinal, then a set
is a limit ordinal, then a set 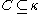 is closed in
is closed in  if and only if
if and only if
for every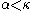 , if
, if 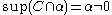 , then
, then 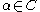 . Thus, if the limit of some sequence
. Thus, if the limit of some sequence
in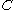 is less than
is less than  , then the limit is also in
, then the limit is also in 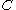 .
.
If is a limit ordinal and
is a limit ordinal and 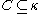 then
then 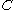 is unbounded in
is unbounded in  if and only if for any
if and only if for any 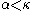 , there is some
, there is some 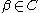 such that
such that 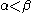 .
.
If a set is both closed and unbounded, then it is a club set. Closed proper classes are also of interest (every proper class of ordinals is unbounded in the class of all ordinals).
For example, the set of all countable limit ordinals is a club set with respect to the first uncountable ordinal
; but it is not a club set with respect to any higher limit ordinal, since it is neither closed nor unbounded.
The set of all limit ordinals is closed unbounded in
is closed unbounded in  (
( regular). In fact a club set is nothing else but the range of a normal function
regular). In fact a club set is nothing else but the range of a normal function
(i.e. increasing and continuous).
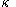 be a limit ordinal of uncountable cofinality
be a limit ordinal of uncountable cofinality
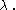 For some
For some  , let
, let 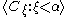 be a sequence of closed unbounded subsets of
be a sequence of closed unbounded subsets of 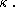 Then
Then  is also closed unbounded. To see this, one can note that an intersection of closed sets is always closed, so we just need to show that this intersection is unbounded. So fix any
is also closed unbounded. To see this, one can note that an intersection of closed sets is always closed, so we just need to show that this intersection is unbounded. So fix any 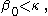 and for each n<ω choose from each
and for each n<ω choose from each 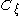 an element
an element 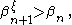 which is possible because each is unbounded. Since this is a collection of fewer than
which is possible because each is unbounded. Since this is a collection of fewer than 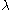 ordinals, all less than
ordinals, all less than 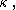 their least upper bound must also be less than
their least upper bound must also be less than 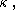 so we can call it
so we can call it 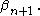 This process generates a countable sequence
This process generates a countable sequence 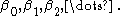 The limit of this sequence must in fact also be the limit of the sequence
The limit of this sequence must in fact also be the limit of the sequence 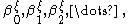 and since each
and since each 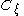 is closed and
is closed and 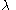 is uncountable, this limit must be in each
is uncountable, this limit must be in each 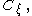 and therefore this limit is an element of the intersection that is above
and therefore this limit is an element of the intersection that is above 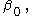 which shows that the intersection is unbounded. QED.
which shows that the intersection is unbounded. QED.
From this, it can be seen that if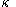 is a regular cardinal, then
is a regular cardinal, then 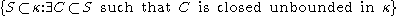 is a non-principal
is a non-principal 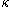 -complete filter
-complete filter
on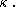
If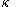 is a regular cardinal then club sets are also closed under diagonal intersection
is a regular cardinal then club sets are also closed under diagonal intersection
.
In fact, if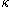 is regular and
is regular and  is any filter on
is any filter on 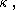 closed under diagonal intersection, containing all sets of the form
closed under diagonal intersection, containing all sets of the form 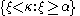 for
for 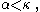 then
then 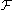 must include all club sets.
must include all club sets.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a club set is a subset of a limit ordinal which is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
under the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
, and is unbounded relative to the limit ordinal. The name club is a contraction of closed and unbounded.
Formal definition
Formally, if is a limit ordinal, then a set
is a limit ordinal, then a set 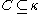 is closed in
is closed in  if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every
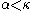 , if
, if 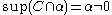 , then
, then 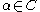 . Thus, if the limit of some sequence
. Thus, if the limit of some sequenceLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in
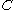 is less than
is less than  , then the limit is also in
, then the limit is also in 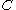 .
.If
 is a limit ordinal and
is a limit ordinal and 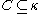 then
then 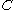 is unbounded in
is unbounded in  if and only if for any
if and only if for any 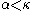 , there is some
, there is some 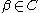 such that
such that 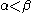 .
.If a set is both closed and unbounded, then it is a club set. Closed proper classes are also of interest (every proper class of ordinals is unbounded in the class of all ordinals).
For example, the set of all countable limit ordinals is a club set with respect to the first uncountable ordinal
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
; but it is not a club set with respect to any higher limit ordinal, since it is neither closed nor unbounded.
The set of all limit ordinals
 is closed unbounded in
is closed unbounded in  (
( regular). In fact a club set is nothing else but the range of a normal function
regular). In fact a club set is nothing else but the range of a normal functionNormal function
In axiomatic set theory, a function f : Ord → Ord is called normal iff it is continuous and strictly monotonically increasing. This is equivalent to the following two conditions:...
(i.e. increasing and continuous).
The closed unbounded filter
Let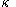 be a limit ordinal of uncountable cofinality
be a limit ordinal of uncountable cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
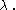 For some
For some  , let
, let 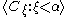 be a sequence of closed unbounded subsets of
be a sequence of closed unbounded subsets of 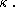 Then
Then  is also closed unbounded. To see this, one can note that an intersection of closed sets is always closed, so we just need to show that this intersection is unbounded. So fix any
is also closed unbounded. To see this, one can note that an intersection of closed sets is always closed, so we just need to show that this intersection is unbounded. So fix any 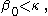 and for each n<ω choose from each
and for each n<ω choose from each 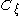 an element
an element 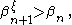 which is possible because each is unbounded. Since this is a collection of fewer than
which is possible because each is unbounded. Since this is a collection of fewer than 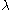 ordinals, all less than
ordinals, all less than 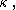 their least upper bound must also be less than
their least upper bound must also be less than 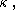 so we can call it
so we can call it 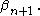 This process generates a countable sequence
This process generates a countable sequence 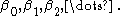 The limit of this sequence must in fact also be the limit of the sequence
The limit of this sequence must in fact also be the limit of the sequence 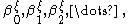 and since each
and since each 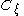 is closed and
is closed and 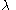 is uncountable, this limit must be in each
is uncountable, this limit must be in each 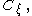 and therefore this limit is an element of the intersection that is above
and therefore this limit is an element of the intersection that is above 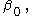 which shows that the intersection is unbounded. QED.
which shows that the intersection is unbounded. QED.From this, it can be seen that if
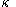 is a regular cardinal, then
is a regular cardinal, then 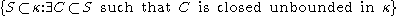 is a non-principal
is a non-principal 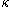 -complete filter
-complete filterFilter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
on
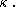
If
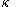 is a regular cardinal then club sets are also closed under diagonal intersection
is a regular cardinal then club sets are also closed under diagonal intersectionDiagonal intersection
Diagonal intersection is a term used in mathematics, especially in set theory.If \displaystyle\delta is an ordinal number and \displaystyle\langle X_\alpha \mid \alphaDiagonal intersection is a term used in mathematics, especially in set theory....
.
In fact, if
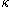 is regular and
is regular and  is any filter on
is any filter on 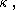 closed under diagonal intersection, containing all sets of the form
closed under diagonal intersection, containing all sets of the form 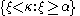 for
for 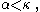 then
then 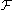 must include all club sets.
must include all club sets.

