Clifford parallel
Encyclopedia
A Clifford parallel is a line which lies at a constant distance from some "base" line but, unlike an ordinary parallel
line, does not lie in the same plane. Such lines do not exist in ordinary Euclidean space
, but only in certain others such as elliptic space.
Clifford parallels were first described in 1873 by the English mathematician William Kingdon Clifford
.
The lines on 1 in elliptic space are described by versors with a fixed axis r: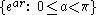
For an arbitrary point u in elliptic space, the right Clifford parallel to this line is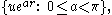
and the left Clifford parallel is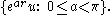
Clifford parallels are also called paratactic lines.
Given two square roots of minus one in the quaternion
s, written r and s, the Clifford surface through them is given by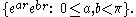
A Clifford surface is a ruled surface
: every point is on two lines, each contained in the surface.
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
line, does not lie in the same plane. Such lines do not exist in ordinary Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, but only in certain others such as elliptic space.
Clifford parallels were first described in 1873 by the English mathematician William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
.
The lines on 1 in elliptic space are described by versors with a fixed axis r:
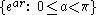
For an arbitrary point u in elliptic space, the right Clifford parallel to this line is
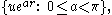and the left Clifford parallel is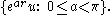Clifford parallels are also called paratactic lines.
Clifford surfaces
Rotating a Clifford parallel around the base line creates a Clifford surface.Given two square roots of minus one in the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, written r and s, the Clifford surface through them is given by
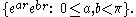
A Clifford surface is a ruled surface
Ruled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
: every point is on two lines, each contained in the surface.