
Clebsch graph
Encyclopedia
In the mathematical
field of graph theory
, the Clebsch graph is an undirected graph with 16 vertices and 40 edges. It is named after Alfred Clebsch
, a German mathematician who discovered it in 1868. It is also known as the Greenwood–Gleason graph after the work of , who used it to evaluate the Ramsey number R(3,3,3) = 17.
. It may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an n-dimensional hypercube, a pair of vertices are opposite if the shortest path between them has n edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by identifying together (or contracting) every opposite pair of vertices.
Another construction, leading to the same graph, is to create a vertex for each element of the finite field
GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a perfect cube.
of degree 5 with parameters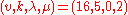 .
.
Its complement is also a strongly regular graph.
The graph is hamiltonian, non planar
and non eulerian. It is also both 5-vertex-connected
and 5-edge-connected
.
The subgraph that is induced by the ten non-neighbors of any vertex in the Clebsch graph forms an isomorphic
copy of the Petersen graph
.
The edges of the complete graph
K16 may be partitioned into three disjoint copies of the Clebsch graph. Because the Clebsch graph is a triangle-free graph
, this shows that there is a triangle-free three-coloring of the edges of K16; that is, that the Ramsey number R(3,3,3) describing the minimum number of vertices in a complete graph without a triangle-free three-coloring is at least 17. used this construction as part of their proof that R(3,3,3) = 17.
The Clebsch graph is the Keller graph
of dimension two, part of a family of graphs used to find tilings of high-dimensional Euclidean space
s by hypercube
s no two of which meet face-to-face.
of the Clebsch graph is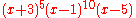 . Therefore the Clebsch graph is an integral graph
. Therefore the Clebsch graph is an integral graph
: its spectrum
consists entirely of integers. The Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
The Clebsch graph is a Cayley graph
with an automorphism group of order 1920, isomorphic to the Coxeter group
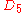 . As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive
. As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive
. In fact, it is arc transitive
, hence edge transitive
and distance transitive
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Clebsch graph is an undirected graph with 16 vertices and 40 edges. It is named after Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
, a German mathematician who discovered it in 1868. It is also known as the Greenwood–Gleason graph after the work of , who used it to evaluate the Ramsey number R(3,3,3) = 17.
Construction
This graph is equivalent to the order-5 folded cube graphFolded cube graph
In graph theory, a folded cube graph is an undirected graph formed from a hypercube graph by adding to it a perfect matching that connects opposite pairs of hypercube vertices.-Construction:...
. It may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an n-dimensional hypercube, a pair of vertices are opposite if the shortest path between them has n edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by identifying together (or contracting) every opposite pair of vertices.
Another construction, leading to the same graph, is to create a vertex for each element of the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a perfect cube.
Properties
The Clebsch graph is a strongly regular graphStrongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
of degree 5 with parameters
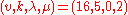 .
.Its complement is also a strongly regular graph.
The graph is hamiltonian, non planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
and non eulerian. It is also both 5-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 5-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
.
The subgraph that is induced by the ten non-neighbors of any vertex in the Clebsch graph forms an isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
copy of the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
.
The edges of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K16 may be partitioned into three disjoint copies of the Clebsch graph. Because the Clebsch graph is a triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
, this shows that there is a triangle-free three-coloring of the edges of K16; that is, that the Ramsey number R(3,3,3) describing the minimum number of vertices in a complete graph without a triangle-free three-coloring is at least 17. used this construction as part of their proof that R(3,3,3) = 17.
The Clebsch graph is the Keller graph
Keller's conjecture
In geometry, Keller's conjecture is the conjecture introduced by that in any tiling of Euclidean space by identical hypercubes there are two cubes that meet face to face. For instance, as shown in the illustration, in any tiling of the plane by identical squares, some two squares must meet edge to...
of dimension two, part of a family of graphs used to find tilings of high-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s by hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s no two of which meet face-to-face.
Algebraic properties
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Clebsch graph is
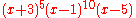 . Therefore the Clebsch graph is an integral graph
. Therefore the Clebsch graph is an integral graphIntegral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
: its spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers. The Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
The Clebsch graph is a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
with an automorphism group of order 1920, isomorphic to the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
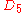 . As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive
. As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitiveVertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
. In fact, it is arc transitive
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
, hence edge transitive
Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
and distance transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
.

