
Clausius-Clapeyron relation
Encyclopedia
The Clausius–Clapeyron relation, named after Rudolf Clausius
and Benoît Paul Émile Clapeyron
, who defined it sometime after 1834, is a way of characterizing a discontinuous phase transition
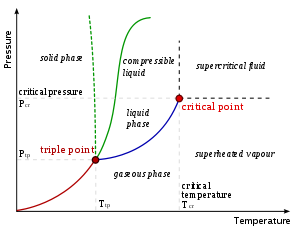
between two phases of matter. On a pressure
–temperature
(P–T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius–Clapeyron relation gives the slope
of this curve. Mathematically,

where is the slope of the coexistence curve,
is the slope of the coexistence curve,  is the latent heat
is the latent heat
, is the temperature
is the temperature
, and is the volume
is the volume
change of the phase transition.
.
, take the specific entropy, for a homogeneous substance to be a function of specific volume,
for a homogeneous substance to be a function of specific volume,  , and temperature,
, and temperature, 

During a phase change, the temperature is constant, so

Using the appropriate Maxwell relation gives

Since temperature and pressure are constant during a phase change, the derivative of pressure with respect to temperature is not a function of the specific volume. Thus the partial derivative may be changed into a total derivative and be factored out when taking an integral from one phase to another,


For a closed system undergoing an internally reversible process, the first law
is

Using the definition of specific enthalpy, and the fact that the temperature and pressure are constant, we have
and the fact that the temperature and pressure are constant, we have

After substitution of this result into the derivative of the pressure, one finds

where the shift to capital letters indicates a shift to extensive variables. This last equation is called the Clausius–Clapeyron equation, though some thermodynamics texts just call it the Clapeyron equation, possibly to distinguish it from the approximation below.
When the transition is to a gas phase, the final specific volume can be many times the size of the initial specific volume. A natural approximation would be to replace with
with  Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law, so that
Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law, so that  where R is the mass specific gas constant (forcing
where R is the mass specific gas constant (forcing  and
and  to be mass specific). Thus,
to be mass specific). Thus,

This leads to a version of the Clausius–Clapeyron equation that is simpler to integrate:

 or
or
These last equations are useful because they relate equilibrium or saturation vapor pressure and temperature to the enthalpy
of phase change, without requiring specific volume data. Note that in this last equation, the subscripts 1 and 2 correspond to different locations on the pressure versus temperature phase lines. In earlier equations, they corresponded to different specific volumes and entropies at the same saturation pressure and temperature.
 Along the coexistence curve, we also have
Along the coexistence curve, we also have  We now use the Gibbs–Duhem relation
We now use the Gibbs–Duhem relation
 where
where  and
and  are, respectively, the entropy
are, respectively, the entropy
and volume per particle, to obtain

Hence, rearranging, we have

From the relation between heat and change of entropy in a reversible process δQ = T dS, we have that the quantity of heat added in the transformation is

Combining the last two equations we obtain the standard relation.

Then assume that p and T are changed, but in such a way that the system is still kept in equilibrium:
Remembering that



By substituting : we get:
we get:
which is the Clapeyron equation.
The Clausius-Clapeyron equation is now obtained by inserting the molar volume of an ideal gas into the equation:
") on the temperature, is complex and difficult to use. Fortunately approximations have been developed.

 is the equilibrium or saturation vapor pressure in hPa, which is a function of temperature;
is the equilibrium or saturation vapor pressure in hPa, which is a function of temperature;  is in Celsius. Since there is only a weak dependence on temperature of the denominator of the exponent, this equation shows that saturation water vapor pressure changes approximately exponentially
is in Celsius. Since there is only a weak dependence on temperature of the denominator of the exponent, this equation shows that saturation water vapor pressure changes approximately exponentially
with .
.

where
This can be used to predict the temperature at a certain pressure, given the temperature at another pressure, or vice versa. Alternatively, if the corresponding temperature and pressure is known at two points, the enthalpy of vaporization can be determined.
The equivalent formulation, in which the values associated with one P,T point are combined into a constant (the constant of integration as above), is
For instance, if the p,T values are known for a series of data points along the phase boundary, then the enthalpy of vaporization may be determined from a plot of against
against 
Notes:

where:
 below 0°C. Note that water is unusual in that its change in volume upon melting is negative. We can assume
below 0°C. Note that water is unusual in that its change in volume upon melting is negative. We can assume

and substituting in
we obtain
 = −13.5 MPa/K.
= −13.5 MPa/K.
To provide a rough example of how much pressure this is, to melt ice at −7 °C (the temperature many ice skating
rinks are set at) would require balancing a small car (mass = 1000 kg) on a thimble
(area = 1 cm²).
Rudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
and Benoît Paul Émile Clapeyron
Benoit Paul Émile Clapeyron
Benoît Paul Émile Clapeyron was a French engineer and physicist, one of the founders of thermodynamics.-Life:...
, who defined it sometime after 1834, is a way of characterizing a discontinuous phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
between two phases of matter. On a pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
–temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
(P–T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius–Clapeyron relation gives the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of this curve. Mathematically,

where
 is the slope of the coexistence curve,
is the slope of the coexistence curve,  is the latent heat
is the latent heatLatent heat
Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was...
,
 is the temperature
is the temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and
 is the volume
is the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
change of the phase transition.
Disambiguation
The generalized equation given in the opening of this article is sometimes called the Clapeyron equation, while a less general form is sometimes called the Clausius–Clapeyron equation. The less general form neglects the magnitude of the specific volume of the liquid (or solid) state relative to that of the gas state and also approximates the specific volume of the gas state via the ideal gas lawIdeal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
.
Derivations

Derivation from state postulate
Using the state postulateThermodynamic state
A thermodynamic state is a set of values of properties of a thermodynamic system that must be specified to reproduce the system. The individual parameters are known as state variables, state parameters or thermodynamic variables. Once a sufficient set of thermodynamic variables have been...
, take the specific entropy,
 for a homogeneous substance to be a function of specific volume,
for a homogeneous substance to be a function of specific volume,  , and temperature,
, and temperature, 

During a phase change, the temperature is constant, so

Using the appropriate Maxwell relation gives

Since temperature and pressure are constant during a phase change, the derivative of pressure with respect to temperature is not a function of the specific volume. Thus the partial derivative may be changed into a total derivative and be factored out when taking an integral from one phase to another,


-
 is used as an operator to represent the change in the variable that follows it—final (2) minus initial (1)
is used as an operator to represent the change in the variable that follows it—final (2) minus initial (1)
For a closed system undergoing an internally reversible process, the first law
First law of thermodynamics
The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
is

Using the definition of specific enthalpy,
 and the fact that the temperature and pressure are constant, we have
and the fact that the temperature and pressure are constant, we have
After substitution of this result into the derivative of the pressure, one finds

where the shift to capital letters indicates a shift to extensive variables. This last equation is called the Clausius–Clapeyron equation, though some thermodynamics texts just call it the Clapeyron equation, possibly to distinguish it from the approximation below.
When the transition is to a gas phase, the final specific volume can be many times the size of the initial specific volume. A natural approximation would be to replace
 with
with  Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law, so that
Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law, so that  where R is the mass specific gas constant (forcing
where R is the mass specific gas constant (forcing  and
and  to be mass specific). Thus,
to be mass specific). Thus,
This leads to a version of the Clausius–Clapeyron equation that is simpler to integrate:

 or
or
-
 is a constant of integration.
is a constant of integration.
These last equations are useful because they relate equilibrium or saturation vapor pressure and temperature to the enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of phase change, without requiring specific volume data. Note that in this last equation, the subscripts 1 and 2 correspond to different locations on the pressure versus temperature phase lines. In earlier equations, they corresponded to different specific volumes and entropies at the same saturation pressure and temperature.
Derivation from Gibbs–Duhem relation
Suppose two phases, I and II, are in contact and at equilibrium with each other. Then the chemical potentials are related by Along the coexistence curve, we also have
Along the coexistence curve, we also have  We now use the Gibbs–Duhem relation
We now use the Gibbs–Duhem relation where
where  and
and  are, respectively, the entropy
are, respectively, the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
and volume per particle, to obtain

Hence, rearranging, we have

From the relation between heat and change of entropy in a reversible process δQ = T dS, we have that the quantity of heat added in the transformation is

Combining the last two equations we obtain the standard relation.
Derivation assuming equilibrium
Suppose we have a system in equilibrium, then:
Then assume that p and T are changed, but in such a way that the system is still kept in equilibrium:

Remembering that




By substituting :
 we get:
we get:
which is the Clapeyron equation.
The Clausius-Clapeyron equation is now obtained by inserting the molar volume of an ideal gas into the equation:

Approximations
An analytical solution to the Clausius-Clapeyron equation, accounting for the weak dependence of the enthalpy of vaporization (or "latent heatLatent heat
Latent heat is the heat released or absorbed by a chemical substance or a thermodynamic system during a process that occurs without a change in temperature. A typical example is a change of state of matter, meaning a phase transition such as the melting of ice or the boiling of water. The term was...
") on the temperature, is complex and difficult to use. Fortunately approximations have been developed.
August-Roche-Magnus approximation
A very good approximation can usually be made using the August-Roche-Magnus formula (usually called the Magnus or Magnus-Tetens approximation, though this is historically inaccurate):
 is the equilibrium or saturation vapor pressure in hPa, which is a function of temperature;
is the equilibrium or saturation vapor pressure in hPa, which is a function of temperature;  is in Celsius. Since there is only a weak dependence on temperature of the denominator of the exponent, this equation shows that saturation water vapor pressure changes approximately exponentially
is in Celsius. Since there is only a weak dependence on temperature of the denominator of the exponent, this equation shows that saturation water vapor pressure changes approximately exponentiallyExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
with
 .
.Chemistry and chemical engineering
The Clausius–Clapeyron equation for the liquid–vapor boundary may be used in either of two equivalent forms.
where
 and
and  are a corresponding temperature (in kelvins or other absolute temperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
are a corresponding temperature (in kelvins or other absolute temperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
units) and vapor pressureVapor pressureVapor pressure or equilibrium vapor pressure is the pressure of a vapor in thermodynamic equilibrium with its condensed phases in a closed system. All liquids have a tendency to evaporate, and some solids can sublimate into a gaseous form... and
and  are the corresponding temperature and pressure at another point
are the corresponding temperature and pressure at another point is the molar enthalpy of vaporization
is the molar enthalpy of vaporization is the gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
is the gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
(8.314 J mol−1K−1)
This can be used to predict the temperature at a certain pressure, given the temperature at another pressure, or vice versa. Alternatively, if the corresponding temperature and pressure is known at two points, the enthalpy of vaporization can be determined.
The equivalent formulation, in which the values associated with one P,T point are combined into a constant (the constant of integration as above), is
For instance, if the p,T values are known for a series of data points along the phase boundary, then the enthalpy of vaporization may be determined from a plot of
 against
against 
Notes:
- As in the derivation above, the enthalpy of vaporization is assumed to be constant over the pressure/temperature range considered
- Equivalent expressions for the solid–vapor boundary are found by replacing the molar enthalpy of vaporization by the molar enthalpy of sublimation,

Meteorology and climatology
Clausius–Clapeyron equations is given for typical atmospheric conditions as
where:
 is saturation water vapor pressure,
is saturation water vapor pressure, is a temperature,
is a temperature, is latent heat of evaporation,
is latent heat of evaporation, is water vapor gas constant.
is water vapor gas constant.
Example
One of the uses of this equation is to determine if a phase transition will occur in a given situation. Consider the question of how much pressure is needed to melt ice at a temperature below 0°C. Note that water is unusual in that its change in volume upon melting is negative. We can assume
below 0°C. Note that water is unusual in that its change in volume upon melting is negative. We can assume
and substituting in
-
 = 3.34 J/kg (latent heat of water),
= 3.34 J/kg (latent heat of water), -
 = 273 KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
= 273 KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
(absolute temperature), and -
 = −9.05 m³/kg (change in volume from solid to liquid),
= −9.05 m³/kg (change in volume from solid to liquid),
we obtain
 = −13.5 MPa/K.
= −13.5 MPa/K.To provide a rough example of how much pressure this is, to melt ice at −7 °C (the temperature many ice skating
Ice skating
Ice skating is moving on ice by using ice skates. It can be done for a variety of reasons, including leisure, traveling, and various sports. Ice skating occurs both on specially prepared indoor and outdoor tracks, as well as on naturally occurring bodies of frozen water, such as lakes and...
rinks are set at) would require balancing a small car (mass = 1000 kg) on a thimble
Thimble
A thimble is a small hard pitted cup worn for protection on the finger that pushes the needle in sewing.The earliest known thimble was Roman and was found at Pompeii. Made of bronze, its creation has been dated to the 1st century AD...
(area = 1 cm²).


