Choice sequence
Encyclopedia
In intuitionistic mathematics
, a choice sequence is a constructive
formulation of a sequence
. Since the Intuitionistic school of mathematics, as formulated by L. E. J. Brouwer, rejects the idea of a completed infinity, in order to use a sequence (which is, in classical mathematics, an infinite object), we must have a formulation of a finite, constructible object which can serve the same purpose as a sequence. Thus, Brouwer formulated the choice sequence, which is given as a construction, rather than an abstract, infinite object.
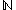can be thought of as a lawlike sequence: the sequence can be fully constructively described by the unique element 0 and a successor function. Given this formulation, we know that the 
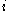th element in the sequence of natural numbers will be the number 
. Similarly, a function
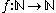mapping from the natural numbers into the natural numbers effectively determines the value for any argument it takes, and thus describes a lawlike sequence.
A lawless (also, free) sequence, on the other hand, is one that is not predetermined. It is to be thought of as a procedure for generating values for the arguments 0, 1, 2, .... That is, a lawless sequence
is a procedure for generating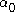 
, 
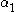, ... (the elements of the sequence 
) such that:
Note that the first point above is slightly misleading, as we may specify, for example, that the values in a sequence be drawn exclusively from the set of natural numbers—we can specify, a priori, the range of the sequence.
The canonical example of a lawless sequence is the series of rolls of a die
. We specify which die to use and, optionally, specify in advance the values of the first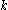
rolls (for 
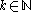). Further, we restrict the values of the sequence to be in the set 
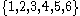. This specification comprises the procedure for generating the lawless sequence in question. At no point, then, is any particular future value of the sequence known.
s in particular that we expect to hold of choice sequences as described above. Let
denote the relation "the sequence 
begins with the initial sequence 
" for choice sequence 
and finite segment 
(more specifically, 
will probably be an integer encoding
a finite initial sequence).
We expect the following, called the axiom of open data, to hold of all lawless sequences:
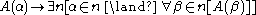
where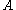
is a one-place predicate. The intuitive justification for this axiom is as follows: in intuionistic mathematics, verification that 
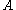holds of the sequence 
is given as a procedure
; at any point of execution of this procedure, we will have examined only a finite initial segment of the sequence. Intuitively, then, this axiom states that since, at any point of verifying that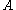
holds of 
, we will only have verified that 
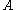holds for a finite initial sequence of 
; thus, it must be the case that 
also holds for any lawless sequence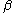 
sharing this initial sequence. This is so because, at any point in the procedure of verifying 
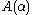, for any such 
sharing the initial prefix of 
encoded by 
that we have already examined, if we run the identical procedure on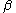 
, we will get the same result. The axiom can be generalized for any predicate taking an arbitrary number of arguments.
Another axiom is required for lawless sequences. The axiom of density, given by:
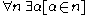
states that, for any finite prefix (encoded by)
, there is some sequence 
beginning with that prefix. We require this axiom so as not to have any "holes" in the set of choice sequences. This axiom is the reason we require that arbitrarily long finite initial sequences of lawless choice sequences can be specified in advance; without this requirement, the axiom of density is not necessarily guaranteed.
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...
, a choice sequence is a constructive
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
formulation of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. Since the Intuitionistic school of mathematics, as formulated by L. E. J. Brouwer, rejects the idea of a completed infinity, in order to use a sequence (which is, in classical mathematics, an infinite object), we must have a formulation of a finite, constructible object which can serve the same purpose as a sequence. Thus, Brouwer formulated the choice sequence, which is given as a construction, rather than an abstract, infinite object.
Lawlike and lawless sequences
A distinction is made between lawless and lawlike sequences. A lawlike sequence is one that can be described completely — it is a completed construction, that can be fully described. For example, the natural numbers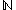 can be thought of as a lawlike sequence: the sequence can be fully constructively described by the unique element 0 and a successor function. Given this formulation, we know that the 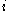th element in the sequence of natural numbers will be the number . Similarly, a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
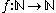mapping from the natural numbers into the natural numbers effectively determines the value for any argument it takes, and thus describes a lawlike sequence.A lawless (also, free) sequence, on the other hand, is one that is not predetermined. It is to be thought of as a procedure for generating values for the arguments 0, 1, 2, .... That is, a lawless sequence
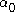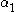is a procedure for generating , , ... (the elements of the sequence ) such that:
- At any given moment of construction of the sequence
, only an initial segment of the sequence is known, and no restrictions are placed on the future values of 
; and - One may specify, in advance, an initial segment
of 
.
Note that the first point above is slightly misleading, as we may specify, for example, that the values in a sequence be drawn exclusively from the set of natural numbers—we can specify, a priori, the range of the sequence.
The canonical example of a lawless sequence is the series of rolls of a die
Dice
A die is a small throwable object with multiple resting positions, used for generating random numbers...
. We specify which die to use and, optionally, specify in advance the values of the first
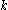rolls (for 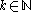). Further, we restrict the values of the sequence to be in the set 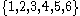. This specification comprises the procedure for generating the lawless sequence in question. At no point, then, is any particular future value of the sequence known.Axiomatization
There are two axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s in particular that we expect to hold of choice sequences as described above. Let
denote the relation "the sequence begins with the initial sequence " for choice sequence and finite segment (more specifically, will probably be an integer encodingNumbering (computability theory)
In computability theory a numbering is the assignment of natural numbers to a set of objects like rational numbers, graphs or words in some language...
a finite initial sequence).
We expect the following, called the axiom of open data, to hold of all lawless sequences:
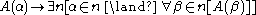
where
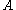is a one-place predicate. The intuitive justification for this axiom is as follows: in intuionistic mathematics, verification that 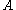holds of the sequence is given as a procedureAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
; at any point of execution of this procedure, we will have examined only a finite initial segment of the sequence. Intuitively, then, this axiom states that since, at any point of verifying that
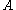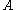holds of , we will only have verified that holds for a finite initial sequence of ; thus, it must be the case that also holds for any lawless sequence 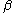sharing this initial sequence. This is so because, at any point in the procedure of verifying 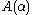, for any such sharing the initial prefix of encoded by that we have already examined, if we run the identical procedure on 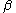, we will get the same result. The axiom can be generalized for any predicate taking an arbitrary number of arguments.Another axiom is required for lawless sequences. The axiom of density, given by:
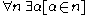
states that, for any finite prefix (encoded by)
, there is some sequence beginning with that prefix. We require this axiom so as not to have any "holes" in the set of choice sequences. This axiom is the reason we require that arbitrarily long finite initial sequences of lawless choice sequences can be specified in advance; without this requirement, the axiom of density is not necessarily guaranteed.