Chiral superfield
Encyclopedia
In theoretical physics
, one often analyzes theories with supersymmetry
in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace
. Superspace contains the usual space-time coordinates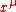
, 
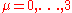, and four extra fermionic coordinates 
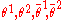, transforming as a two-component (Weyl) spinor
and its conjugate.
In N=1 supersymmetry
in 3+1D, a chiral superfield is a function over chiral superspace. There exists a projection from the (full) superspace to chiral superspace. So, a function over chiral
superspace can be pulled back to the full superspace. Such a function satisfies the covariant constraint
. Similarly, we also have an antichiral superspace which is the complex conjugate of chiral superspace and antichiral superfields.
Superspace is the homogeneous space
of the SUSY supergroup with the Lorentz group
as the stabilizer. Chiral superspace is the homogeneous space with the supergroup generated by the Lorentz
transformations and
as the stabilizer. Clearly, there is a projection
from the former to the latter.
Every superfield—i.e. a field that depends on all coordinates of the superspace—may be expanded with respect to the fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfields, that, in the chiral representation of supersymmetry, depend only on the variables
but not their conjugates. See also F-term
s.
Chiral superfields satisfy the relation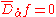
. They can also be expressed as fields over chiral superspace.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, one often analyzes theories with supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
. Superspace contains the usual space-time coordinates
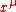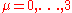, , and four extra fermionic coordinates 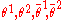, transforming as a two-component (Weyl) spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
and its conjugate.
In N=1 supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
in 3+1D, a chiral superfield is a function over chiral superspace. There exists a projection from the (full) superspace to chiral superspace. So, a function over chiral
superspace can be pulled back to the full superspace. Such a function satisfies the covariant constraint
. Similarly, we also have an antichiral superspace which is the complex conjugate of chiral superspace and antichiral superfields.Superspace is the homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
of the SUSY supergroup with the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
as the stabilizer. Chiral superspace is the homogeneous space with the supergroup generated by the Lorentz
transformations and
as the stabilizer. Clearly, there is a projectionProjection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
from the former to the latter.
Every superfield—i.e. a field that depends on all coordinates of the superspace—may be expanded with respect to the fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfields, that, in the chiral representation of supersymmetry, depend only on the variables
but not their conjugates. See also F-termF-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s.
Chiral superfields satisfy the relation
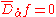. They can also be expressed as fields over chiral superspace.See also
- vector superfield
- current superfield
- F-termF-termIn theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
- superpotentialSuperpotentialSuperpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...