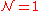SUSY in 4D

In theoretical physics

Theoretical physics

Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...

, one often analyzes theories with supersymmetry

Supersymmetry

In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...

 which also have
internal gauge symmetries. So, it is important to come up with a supersymmetric generalization
of gauge theories.
In four dimensions, the minimal N=1 supersymmetry may be written using a superspace

Superspace

"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....

. This superspace involves four extra fermionic coordinates 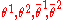, transforming as a two-component spinor

Spinor

In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...

 and its conjugate.

Every superfield, i.e. a field that depends on all coordinates of the superspace, may be expanded with respect to the new fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfield

Chiral superfield

In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...

s, that only depend on the variables but not their conjugates (more precisely, 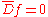). However, a vector superfield depends on all coordinates. It describes a gauge field and its superpartner

Superpartner

In particle physics, a superpartner is a hypothetical elementary particle. Supersymmetry is one of the synergistic theories in current high-energy physics which predicts the existence of these "shadow" particles....

, namely a Weyl fermion that obeys a Dirac equation

Dirac equation

The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...

.


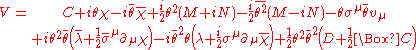
V is the vector superfield (prepotential) and is real (). The fields on the right hand side are component fields.

The gauge transformations act as
where Λ is any chiral superfield.

It's easy to check that the chiral superfield
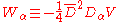
is gauge invariant. So is its complex conjugate .

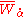A nonSUSY covariant gauge which is often used is the Wess-Zumino gauge

Wess-Zumino gauge

In particle physics, the Wess–Zumino gauge is a particular choice of a gauge transformation in a gauge theory with supersymmetry. In this gauge, the supersymmetrized gauge transformation is chosen in such a way that most components of the vector superfield vanish, except for the usual physical...

. Here, C, χ, M and N are
all set to zero. The residual gauge symmetries are gauge transformations of the traditional bosonic
type.

A chiral superfield X with a charge of q transforms as
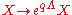
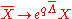
The following term is therefore gauge invariant

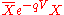
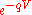is called a bridge since it "bridges" a field which transforms under Λ only with a field which transforms under only.

More generally, if we have a real gauge group G that we wish to supersymmetrize, we first have to complexify it to G^c. e^-qV then acts a compensator for the complex gauge transformations in effect absorbing them leaving only the real parts. This is what's being done in the Wess-Zumino gauge.

Differential superforms

Let's rephrase everything to look more like a conventional Yang-Mill gauge theory. We have a U(1) gauge symmetry acting upon full superspace with a 1-superform gauge connection A. In the analytic basis for the tangent space, the covariant derivative is given by . Integrability conditions for chiral superfields with the chiral constraint 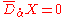leave us with 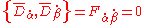. A similar constraint for antichiral superfields leaves us with 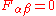. This means that we can either gauge fix 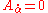or 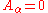but not both simultaneously. Call the two different gauge fixing schemes I and II respectively. In gauge I, 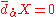and in gauge II, 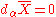. Now, the trick is to use two different gauges simultaneously; gauge I for chiral superfields and gauge II for antichiral superfields. In order to bridge between the two different gauges, we need a gauge transformation. Call it e^-V (by convention). If we were using one gauge for all fields, would be gauge invariant. However, we need to convert gauge I to gauge II, transforming X to (e^-V)^qX. So, the gauge invariant quantity is .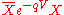

In gauge I, we still have the residual gaug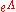e where 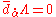and in gauge II, we have the residual gauge 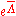satisfying 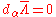. Under the residual gauges, the bridge transforms as 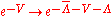. Without any additional constraints, the bridge 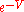wouldn't give all the information about the gauge field. However, with the additional constraint 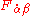, there's only one unique gauge field which is compatible with the bridge modulo gauge transformations. Now, the bridge gives exactly the same information content as the gauge field.

Theories with 8 or more SUSY generators

In theories with higher supersymmetry (and perhaps higher dimension), a vector superfield typically describes not only a gauge field and a Weyl fermion but also at least one complex scalar field

Scalar field

In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...

.

See also

• super QCD
  Super QCD
  In theoretical physics, super QCD is a supersymmetric gauge theory which resembles quantum chromodynamics but contains additional particles and interactions which render it supersymmetric....
  
  
• superpotential
  Superpotential
  Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
  
  
• D-term
  D-term
  In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
  
  
• F-term
  F-term
  In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
  
  
• current superfield.