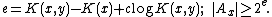Chain rule for Kolmogorov complexity
Encyclopedia
The chain rule for Kolmogorov complexity
is an analogue of the chain rule for information entropy
, which states:
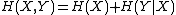
That is, the combined randomness
of two sequences X and Y is the sum of the randomness of X plus whatever randomness is left in Y once we know X.
This follows immediately from the definitions of conditional
and joint entropy fact from probability theory
that the joint probability is the product of the marginal and conditional probability
:
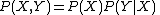
The equivalent statement for Kolmogorov complexity does not hold exactly; it is only true up to a logarithm
ic factor:
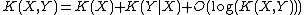
(An exact version, KP(X, Y) = KP(X) + KP(Y|X*) + O(1),
holds for the prefix complexity KP, where X* is a shortest program for X.)
It states that the shortest program to reproduce X and Y is using a program to reproduce X and a program to reproduce Y given X, plus at most a logarithmic factor. Using this statement one can define an analogue of mutual information for Kolmogorov complexity.
access to x, and (whence the log term) the length of one of the programs, so
that we know where to separate the two programs for x and y|x (log(K(x, y)) upper-bounds this length).
The ≥ direction is rather more difficult. The key to the proof is the
construction of the set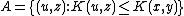
; that is, the
construction of the set of all pairs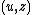
such that the shortest input (for
a universal Turing machine
) that produces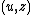
(and some way to distinguish
from 
) is shorter than the shortest producing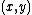 
. We will also
need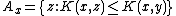
, the subset of 
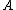where 
.
Enumerating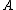
is not hard (although not fast!). In parallel, simulate all
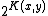programs with length 
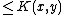. Output each 
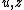as the
simulated program terminates; eventually, any particular such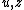
will be
produced. We can restrict to Ax simply by ignoring any output where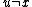
. We will assume that the inequality does not hold and derive a contradiction by finding a short description for K(x) in terms of its index in the enumeration of a subset of A.
In particular, we can describe y by giving the index in which y is output when enumerating Ax (which is less than or equal to |Ax|) along with x and the value of K(x, y). Thus,
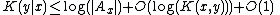
where the O(1) term is from the overhead of the enumerator, which does not depend on x or y.
Assume by way of contradiction
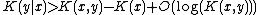
for some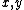
.
Combining this with the above, we have
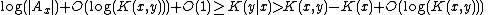
So for any constant c and some x, y,
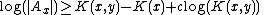
Let
Now, we can enumerate a set of possible values for
by finding all 
such
that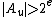
-- list only the 
such that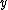 
is output after more than
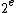other values when enumerating 
. 
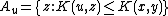is
one such
. Let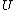 
be the set of all such 
. We can enumerate 
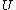by
enumerating each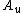
(in parallel, as usual) and outputting a 
only when
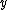would be output for 
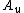and more than 
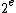other values for the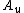 
would be output. Note that given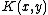
, 
and the index of 
in 
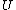we
can enumerate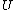
to recover 
.
Note that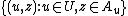
is a subset of 
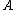, and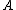 
has at
most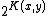
elements, since there are only that many programs of length
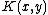. So we have:
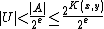
where the first inequality follows since each element of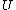
corresponds to an
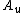with strictly more than 
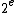elements.
But this leads to a contradiction:
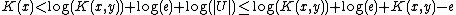
which when we substitute in
gives
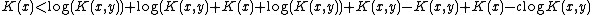
which for large enough
gives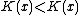 
.
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
is an analogue of the chain rule for information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
, which states:
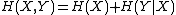
That is, the combined randomness
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
of two sequences X and Y is the sum of the randomness of X plus whatever randomness is left in Y once we know X.
This follows immediately from the definitions of conditional
Conditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
and joint entropy fact from probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
that the joint probability is the product of the marginal and conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
:
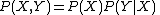
The equivalent statement for Kolmogorov complexity does not hold exactly; it is only true up to a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic factor:
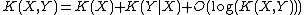
(An exact version, KP(X, Y) = KP(X) + KP(Y|X*) + O(1),
holds for the prefix complexity KP, where X* is a shortest program for X.)
It states that the shortest program to reproduce X and Y is using a program to reproduce X and a program to reproduce Y given X, plus at most a logarithmic factor. Using this statement one can define an analogue of mutual information for Kolmogorov complexity.
Proof
The ≤ direction is obvious: we can write a program to produce x and y by concatenating a program to produce x, a program to produce y givenaccess to x, and (whence the log term) the length of one of the programs, so
that we know where to separate the two programs for x and y|x (log(K(x, y)) upper-bounds this length).
The ≥ direction is rather more difficult. The key to the proof is the
construction of the set
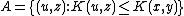; that is, theconstruction of the set of all pairs
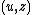such that the shortest input (fora universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
) that produces
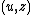(and some way to distinguish from ) is shorter than the shortest producing 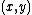. We will alsoneed
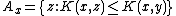, the subset of 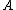where .Enumerating
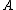is not hard (although not fast!). In parallel, simulate all 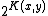programs with length 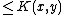. Output each 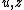as thesimulated program terminates; eventually, any particular such
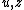will beproduced. We can restrict to Ax simply by ignoring any output where
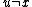. We will assume that the inequality does not hold and derive a contradiction by finding a short description for K(x) in terms of its index in the enumeration of a subset of A.In particular, we can describe y by giving the index in which y is output when enumerating Ax (which is less than or equal to |Ax|) along with x and the value of K(x, y). Thus,
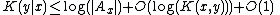
where the O(1) term is from the overhead of the enumerator, which does not depend on x or y.
Assume by way of contradiction
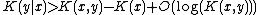
for some
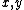.Combining this with the above, we have
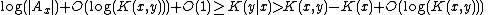
So for any constant c and some x, y,
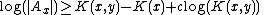
Let
Now, we can enumerate a set of possible values for
by finding all suchthat
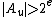-- list only the such that 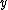is output after more than 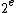other values when enumerating 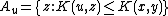. isone such
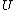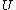. Let be the set of all such . We can enumerate byenumerating each
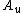(in parallel, as usual) and outputting a only when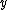 would be output for 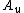and more than 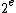other values for the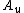 would be output. Note that given
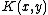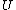, and the index of in wecan enumerate
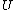to recover .Note that
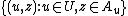is a subset of 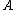, and 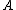has atmost
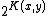elements, since there are only that many programs of length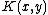. So we have: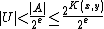where the first inequality follows since each element of
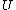corresponds to an 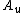with strictly more than 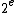elements.But this leads to a contradiction:
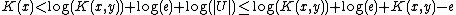
which when we substitute in
gives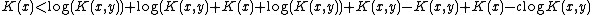which for large enough
gives 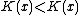.