
Joint entropy
Encyclopedia
Joint entropy is a measure of the uncertainty associated with a set of variables.
 and
and  is defined as
is defined as
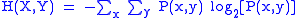
where and
and 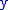 are particular values of
are particular values of  and
and  , respectively,
, respectively, 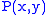 is the probability of these values occurring together, and
is the probability of these values occurring together, and 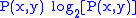 is defined to be 0 if
is defined to be 0 if 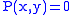 .
.
For more than two variables this expands to
this expands to
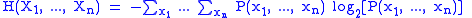
where are particular values of
are particular values of  , respectively,
, respectively,  is the probability of these values occurring together, and
is the probability of these values occurring together, and 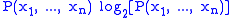 is defined to be 0 if
is defined to be 0 if 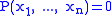 .
.
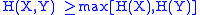
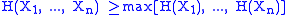
 and
and  are statistically independent.
are statistically independent.
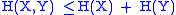
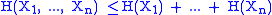
--
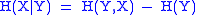
-- and mutual information
:

In quantum information theory, the joint entropy is generalized into the joint quantum entropy
.
Definition
The joint entropy of two variables and
and  is defined as
is defined as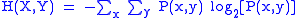
where
 and
and 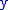 are particular values of
are particular values of  and
and  , respectively,
, respectively, 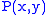 is the probability of these values occurring together, and
is the probability of these values occurring together, and 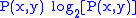 is defined to be 0 if
is defined to be 0 if 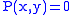 .
.For more than two variables
 this expands to
this expands to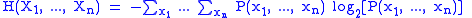
where
 are particular values of
are particular values of  , respectively,
, respectively,  is the probability of these values occurring together, and
is the probability of these values occurring together, and 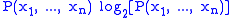 is defined to be 0 if
is defined to be 0 if 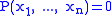 .
.Greater than individual entropies
The joint entropy of a set of variables is greater than or equal to all of the individual entropies of the variables in the set.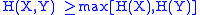
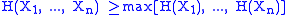
Less than sum of individual entropies
The joint entropy of a set of variables is less than or equal to the sum of the individual entropies of the variables in the set. This is an example of subadditivity. This inequality is an equality if and only if and
and  are statistically independent.
are statistically independent.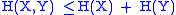
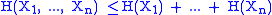
Relations to Other Entropy Measures
Joint entropy is used in the definition of conditional entropyConditional entropy
In information theory, the conditional entropy quantifies the remaining entropy of a random variable Y given that the value of another random variable X is known. It is referred to as the entropy of Y conditional on X, and is written H...
--
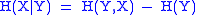
-- and mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
:

In quantum information theory, the joint entropy is generalized into the joint quantum entropy
Joint quantum entropy
The joint quantum entropy generalizes the classical joint entropy to the context of quantum information theory. Intuitively, given two quantum states \rho and \sigma, represented as density operators that are subparts of a quantum system, the joint quantum entropy is a measure of the total...
.

