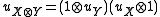Centre (category)
Encyclopedia
Let 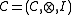 be a monoidal category
be a monoidal category
. The centre of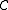 , denoted
, denoted 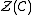 , is the category whose objects are pairs (A,u) consisting of an object A of
, is the category whose objects are pairs (A,u) consisting of an object A of 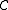 and a natural isomorphism
and a natural isomorphism 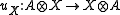 satisfying
satisfying
and
An arrow from (A,u) to (B,v) in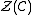 consists of an arrow
consists of an arrow 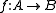 in
in 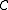 such that
such that
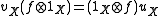 .
.
The category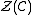 becomes a braided monoidal category with the tensor product on objects defined as
becomes a braided monoidal category with the tensor product on objects defined as

where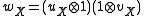 , and the obvious braiding .
, and the obvious braiding .
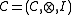 be a monoidal category
be a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
. The centre of
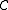 , denoted
, denoted 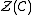 , is the category whose objects are pairs (A,u) consisting of an object A of
, is the category whose objects are pairs (A,u) consisting of an object A of 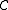 and a natural isomorphism
and a natural isomorphism 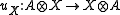 satisfying
satisfyingand
-
 (this is actually a consequence of the first axiom).
(this is actually a consequence of the first axiom).
An arrow from (A,u) to (B,v) in
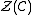 consists of an arrow
consists of an arrow 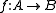 in
in 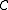 such that
such that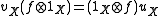 .
.The category
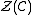 becomes a braided monoidal category with the tensor product on objects defined as
becomes a braided monoidal category with the tensor product on objects defined as
where
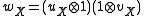 , and the obvious braiding .
, and the obvious braiding .