
Cauchy's functional equation
Encyclopedia
Cauchy's functional equation is the functional equation
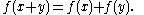
Solutions to this are called additive function
s.
Over the rational numbers, it can be shown using elementary algebra that there is a single family of solutions, namely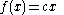 for any arbitrary rational number
for any arbitrary rational number  .
.
Over the real number
s, this is still a family of solutions; however there can exist other solutions that are extremely complicated. Further constraints on f sometimes preclude other solutions, for example:
On the other hand, if no further conditions are imposed on f, then (assuming the axiom of choice) there are infinitely many other functions that satisfy the equation. This was proved in 1905 by Georg Hamel
using Hamel bases. Such functions are sometimes called Hamel functions.
The fifth problem
on Hilbert's list
is a generalisation of this equation. Functions where there exists a real number
 such that
such that  are known as Cauchy-Hamel functions and are used in Dehn-Hadwiger invariants which are used in the extension of Hilbert's third problem
are known as Cauchy-Hamel functions and are used in Dehn-Hadwiger invariants which are used in the extension of Hilbert's third problem
from 3-D to higher dimensions.
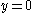 :
:
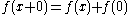
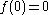
Then put :
:

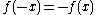
Then by repeated application of the function equation to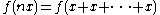 we get:
we get:
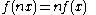
And by replacing with
with 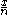 :
:
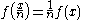
For any rational number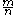 , and by putting
, and by putting 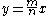 :
:

Putting this all together, we get:
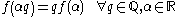
Putting we get the unique family of solutions over
we get the unique family of solutions over  .
.
functions. In particular,
we show that any other solution must have the property that its graph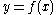 is
is
dense
in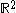 , i.e. that any disk in the plane (however
, i.e. that any disk in the plane (however
small) contains a point from the graph. From this it is easy to prove the various conditions
given in the introductory paragraph.
Suppose without loss of generality that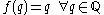 ,
,
and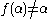 for some
for some 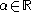 .
.
Then put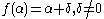 .
.
We now show how to find a point in an arbitrary circle, centre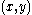 ,
,
radius where
where 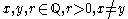 .
.
Put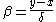 and choose a rational number
and choose a rational number
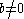 close to
close to  with:
with:
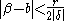
Then choose a rational number close to
close to  with:
with:
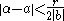
Now put:
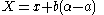

Then using the functional equation, we get:
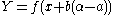
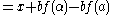
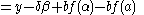
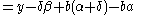
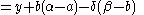
Because of our choices above, the point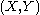 is inside the circle.
is inside the circle.
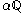 , a scaled copy of the rationals.
, a scaled copy of the rationals.
We can use this to find all solutions to the equation.
Note that this method is highly non-constructive, relying
as it does on the axiom of choice.
If we assume the axiom of choice, there is a basis for the reals over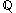
i.e. a set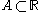 such that
such that
for every real number there is a unique finite set
there is a unique finite set
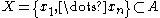 and sequence
and sequence
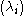 in
in 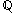
such that:
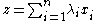
By the argument above, on each copy of the rationals,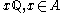 ,
, 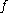 must coincide with a linear map, say with constant of proportionality g(x). In other words, f(y) = g(x)y for every y which is a rational multiple of x. Then by use of the decomposition above and repeated application of the functional equation, we can obtain the value of the function for any real number:
must coincide with a linear map, say with constant of proportionality g(x). In other words, f(y) = g(x)y for every y which is a rational multiple of x. Then by use of the decomposition above and repeated application of the functional equation, we can obtain the value of the function for any real number:
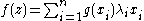
f(z) is a solution to the functional equation for any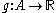 , and every solution is of this form. f is linear if and only if g is constant.
, and every solution is of this form. f is linear if and only if g is constant.
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
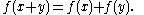
Solutions to this are called additive function
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
s.
Over the rational numbers, it can be shown using elementary algebra that there is a single family of solutions, namely
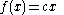 for any arbitrary rational number
for any arbitrary rational number  .
.Over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, this is still a family of solutions; however there can exist other solutions that are extremely complicated. Further constraints on f sometimes preclude other solutions, for example:
- if f is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(proven by Cauchy in 1821). This condition was weakened in 1875 by Darboux who showed that it was only necessary for the function to be continuous at one point. - if f is monotonicMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
on any interval. - if f is boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
on any interval.
On the other hand, if no further conditions are imposed on f, then (assuming the axiom of choice) there are infinitely many other functions that satisfy the equation. This was proved in 1905 by Georg Hamel
Georg Hamel
Georg Karl Wilhelm Hamel was a German mathematician with interests in mechanics, the foundations of mathematics and function theory....
using Hamel bases. Such functions are sometimes called Hamel functions.
The fifth problem
Hilbert's fifth problem
Hilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...
on Hilbert's list
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
is a generalisation of this equation. Functions where there exists a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 such that
such that  are known as Cauchy-Hamel functions and are used in Dehn-Hadwiger invariants which are used in the extension of Hilbert's third problem
are known as Cauchy-Hamel functions and are used in Dehn-Hadwiger invariants which are used in the extension of Hilbert's third problemHilbert's third problem
The third on Hilbert's list of mathematical problems, presented in 1900, is the easiest one. The problem is related to the following question: given any two polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the...
from 3-D to higher dimensions.
Proof of solution over rationals
First put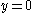 :
: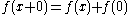
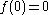
Then put
 :
:
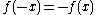
Then by repeated application of the function equation to
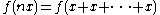 we get:
we get: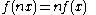
And by replacing
 with
with 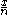 :
: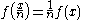
For any rational number
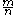 , and by putting
, and by putting 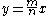 :
:
Putting this all together, we get:
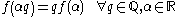
Putting
 we get the unique family of solutions over
we get the unique family of solutions over  .
.Properties of other solutions
We prove below that any other solutions must be highly pathologicalPathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
functions. In particular,
we show that any other solution must have the property that its graph
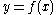 is
isdense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in
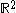 , i.e. that any disk in the plane (however
, i.e. that any disk in the plane (howeversmall) contains a point from the graph. From this it is easy to prove the various conditions
given in the introductory paragraph.
Suppose without loss of generality that
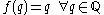 ,
,and
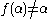 for some
for some 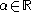 .
.Then put
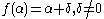 .
.We now show how to find a point in an arbitrary circle, centre
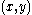 ,
,radius
 where
where 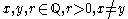 .
.Put
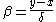 and choose a rational number
and choose a rational number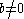 close to
close to  with:
with: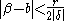
Then choose a rational number
 close to
close to  with:
with: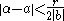
Now put:
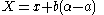

Then using the functional equation, we get:
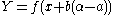
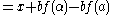
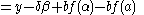
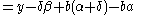
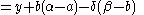
Because of our choices above, the point
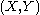 is inside the circle.
is inside the circle.Proof of the existence of other solutions
The linearity proof given above also applies to any set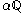 , a scaled copy of the rationals.
, a scaled copy of the rationals.We can use this to find all solutions to the equation.
Note that this method is highly non-constructive, relying
as it does on the axiom of choice.
If we assume the axiom of choice, there is a basis for the reals over
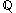
i.e. a set
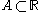 such that
such thatfor every real number
 there is a unique finite set
there is a unique finite set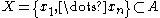 and sequence
and sequence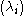 in
in 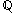
such that:
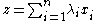
By the argument above, on each copy of the rationals,
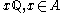 ,
, 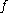 must coincide with a linear map, say with constant of proportionality g(x). In other words, f(y) = g(x)y for every y which is a rational multiple of x. Then by use of the decomposition above and repeated application of the functional equation, we can obtain the value of the function for any real number:
must coincide with a linear map, say with constant of proportionality g(x). In other words, f(y) = g(x)y for every y which is a rational multiple of x. Then by use of the decomposition above and repeated application of the functional equation, we can obtain the value of the function for any real number: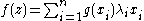
f(z) is a solution to the functional equation for any
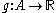 , and every solution is of this form. f is linear if and only if g is constant.
, and every solution is of this form. f is linear if and only if g is constant.External links
- Solution to the Cauchy Equation Rutgers University
- The Hunt for Addi(c)tive Monster

