
Canonical correlation
Encyclopedia
In statistics
, canonical correlation analysis, introduced by Harold Hotelling
, is a way of making sense of cross-covariance matrices. If we have two sets of variables,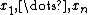 and
and 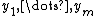 , and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the
, and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the 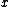 's and the
's and the 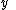 's which have maximum correlation with each other.
's which have maximum correlation with each other.
 and
and  of random variables
of random variables
with finite second moments, one may define the cross-covariance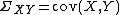 to be the
to be the 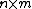 matrix
matrix
whose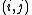 entry is the covariance
entry is the covariance
 . In practice, we would estimate the covariance matrix based on sampled data from
. In practice, we would estimate the covariance matrix based on sampled data from 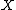 and
and 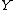 (i.e. from a pair of data matrices).
(i.e. from a pair of data matrices).
Canonical correlation analysis seeks vectors and
and 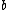 such that the random variables
such that the random variables 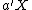 and
and 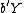 maximize the correlation
maximize the correlation
 . The random variables
. The random variables 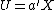 and
and 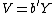 are the first pair of canonical variables. Then one seeks vectors maximizing the same correlation subject to the constraint that they are to be uncorrelated with the first pair of canonical variables; this gives the second pair of canonical variables. This procedure may be continued up to
are the first pair of canonical variables. Then one seeks vectors maximizing the same correlation subject to the constraint that they are to be uncorrelated with the first pair of canonical variables; this gives the second pair of canonical variables. This procedure may be continued up to 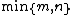 times.
times.
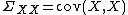 and
and 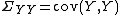 . The parameter to maximize is
. The parameter to maximize is
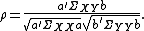
The first step is to define a change of basis
and define
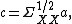
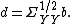
And thus we have
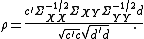
By the Cauchy-Schwarz inequality, we have
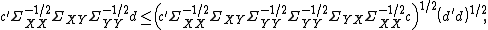

There is equality if the vectors and
and 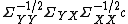 are collinear. In addition, the maximum of correlation is attained if
are collinear. In addition, the maximum of correlation is attained if  is the eigenvector with the maximum eigenvalue for the matrix
is the eigenvector with the maximum eigenvalue for the matrix 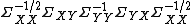 (see Rayleigh quotient). The subsequent pairs are found by using eigenvalues of decreasing magnitudes. Orthogonality is guaranteed by the symmetry of the correlation matrices.
(see Rayleigh quotient). The subsequent pairs are found by using eigenvalues of decreasing magnitudes. Orthogonality is guaranteed by the symmetry of the correlation matrices.
Reciprocally, there is also:
Reversing the change of coordinates, we have that
The canonical variables are defined by:

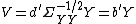
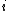 is zero implies all further correlations are also zero. If we have
is zero implies all further correlations are also zero. If we have 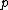 independent observations in a sample and
independent observations in a sample and 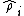 is the estimated correlation for
is the estimated correlation for 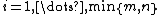 . For the
. For the 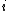 th row, the test statistic is:
th row, the test statistic is:
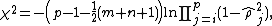
which is asymptotically distributed as a chi-squared with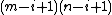 degrees of freedom
degrees of freedom
for large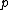 . Since all the correlations from
. Since all the correlations from 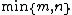 to
to 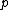 are logically zero (and estimated that way also) the product for the terms after this point is irrelevant.
are logically zero (and estimated that way also) the product for the terms after this point is irrelevant.
and the NEO. By seeing how the MMPI factors relate to the NEO factors, you could gain insight into what dimensions were common between the tests and how much variance was shared. For example you might find that an extraversion
or neuroticism
dimension accounted for a substantial amount of shared variance between the two tests.
One can also use canonical correlation analysis to produce a model equation which relates two sets of variables, for example a set of performance measures and a set of explanatory variables, or a set of outputs and set of inputs. Constraint restrictions can be imposed on such a model to ensure it reflects theoretical requirements or intuitively obvious conditions. This type of model is known as a maximum correlation model.
Visualization of the results of canonical correlation is usually through bar plots of the coefficients of the two sets of variables for the pairs of canonical variates showing significant correlation. Some authors suggest that they are best visualized by plotting them as heliographs, a circular format with ray like bars, with each half representing the two sets of variables.
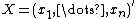 and
and  have zero expected value
have zero expected value
s, i.e.,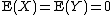 , their covariance
, their covariance
matrices and
and 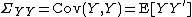 can be viewed as Gram matrices in an inner product, see Covariance#Relationship to inner products, for the columns of
can be viewed as Gram matrices in an inner product, see Covariance#Relationship to inner products, for the columns of  and
and  , correspondingly. The definition of the canonical variables
, correspondingly. The definition of the canonical variables 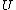 and
and 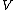 is equivalent to the definition of principal vectors
is equivalent to the definition of principal vectors
for the pair of subspaces spanned by the columns of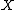 and
and 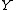 with respect to this inner product. The canonical correlations
with respect to this inner product. The canonical correlations  is equal to the cosine of principal angles
is equal to the cosine of principal angles
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, canonical correlation analysis, introduced by Harold Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
, is a way of making sense of cross-covariance matrices. If we have two sets of variables,
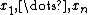 and
and 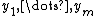 , and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the
, and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the 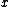 's and the
's and the 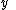 's which have maximum correlation with each other.
's which have maximum correlation with each other.Definition
Given two column vectors and
and  of random variables
of random variablesRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with finite second moments, one may define the cross-covariance
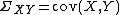 to be the
to be the 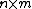 matrix
matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose
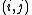 entry is the covariance
entry is the covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
 . In practice, we would estimate the covariance matrix based on sampled data from
. In practice, we would estimate the covariance matrix based on sampled data from 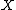 and
and 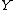 (i.e. from a pair of data matrices).
(i.e. from a pair of data matrices).Canonical correlation analysis seeks vectors
 and
and 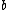 such that the random variables
such that the random variables 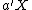 and
and 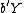 maximize the correlation
maximize the correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
 . The random variables
. The random variables 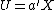 and
and 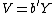 are the first pair of canonical variables. Then one seeks vectors maximizing the same correlation subject to the constraint that they are to be uncorrelated with the first pair of canonical variables; this gives the second pair of canonical variables. This procedure may be continued up to
are the first pair of canonical variables. Then one seeks vectors maximizing the same correlation subject to the constraint that they are to be uncorrelated with the first pair of canonical variables; this gives the second pair of canonical variables. This procedure may be continued up to 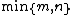 times.
times.Proof
Let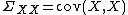 and
and 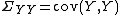 . The parameter to maximize is
. The parameter to maximize is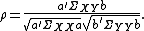
The first step is to define a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
and define
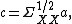
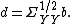
And thus we have
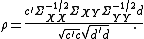
By the Cauchy-Schwarz inequality, we have
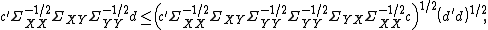

There is equality if the vectors
 and
and 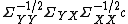 are collinear. In addition, the maximum of correlation is attained if
are collinear. In addition, the maximum of correlation is attained if  is the eigenvector with the maximum eigenvalue for the matrix
is the eigenvector with the maximum eigenvalue for the matrix 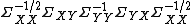 (see Rayleigh quotient). The subsequent pairs are found by using eigenvalues of decreasing magnitudes. Orthogonality is guaranteed by the symmetry of the correlation matrices.
(see Rayleigh quotient). The subsequent pairs are found by using eigenvalues of decreasing magnitudes. Orthogonality is guaranteed by the symmetry of the correlation matrices.Solution
The solution is therefore:-
 is an eigenvector of
is an eigenvector of 
-
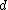 is proportional to
is proportional to 
Reciprocally, there is also:
-
 is an eigenvector of
is an eigenvector of 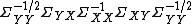
-
 is proportional to
is proportional to 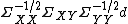
Reversing the change of coordinates, we have that
-
 is an eigenvector of
is an eigenvector of 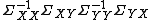
-
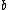 is an eigenvector of
is an eigenvector of 
-
 is proportional to
is proportional to 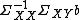
-
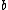 is proportional to
is proportional to 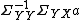
The canonical variables are defined by:

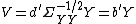
Hypothesis testing
Each row can be tested for significance with the following method. Since the correlations are sorted, saying that row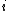 is zero implies all further correlations are also zero. If we have
is zero implies all further correlations are also zero. If we have 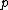 independent observations in a sample and
independent observations in a sample and 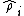 is the estimated correlation for
is the estimated correlation for 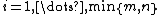 . For the
. For the 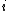 th row, the test statistic is:
th row, the test statistic is: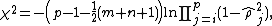
which is asymptotically distributed as a chi-squared with
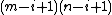 degrees of freedom
degrees of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
for large
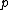 . Since all the correlations from
. Since all the correlations from 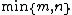 to
to 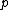 are logically zero (and estimated that way also) the product for the terms after this point is irrelevant.
are logically zero (and estimated that way also) the product for the terms after this point is irrelevant.Practical uses
A typical use for canonical correlation in the experimental context is to take two sets of variables and see what is common amongst the two sets. For example in psychological testing, you could take two well established multidimensional personality tests such as the MMPIMMPI
MMPI may refer to:*Minnesota Multiphasic Personality Inventory, one of the most frequently used personality tests in mental health*Matrix metalloproteinase inhibitor, inhibits cell migration and has antiangiogenic effects...
and the NEO. By seeing how the MMPI factors relate to the NEO factors, you could gain insight into what dimensions were common between the tests and how much variance was shared. For example you might find that an extraversion
Extraversion and introversion
The trait of extraversion-introversion is a central dimension of human personality theories.Extraverts tend to be gregarious, assertive, and interested in seeking out external stimulus. Introverts, in contrast, tend to be introspective, quiet and less sociable. They are not necessarily loners but...
or neuroticism
Neuroticism
Neuroticism is a fundamental personality trait in the study of psychology. It is an enduring tendency to experience negative emotional states. Individuals who score high on neuroticism are more likely than the average to experience such feelings as anxiety, anger, guilt, and depressed mood...
dimension accounted for a substantial amount of shared variance between the two tests.
One can also use canonical correlation analysis to produce a model equation which relates two sets of variables, for example a set of performance measures and a set of explanatory variables, or a set of outputs and set of inputs. Constraint restrictions can be imposed on such a model to ensure it reflects theoretical requirements or intuitively obvious conditions. This type of model is known as a maximum correlation model.
Visualization of the results of canonical correlation is usually through bar plots of the coefficients of the two sets of variables for the pairs of canonical variates showing significant correlation. Some authors suggest that they are best visualized by plotting them as heliographs, a circular format with ray like bars, with each half representing the two sets of variables.
Connection to principal angles
Assuming that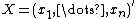 and
and  have zero expected value
have zero expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s, i.e.,
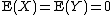 , their covariance
, their covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
matrices
 and
and 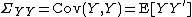 can be viewed as Gram matrices in an inner product, see Covariance#Relationship to inner products, for the columns of
can be viewed as Gram matrices in an inner product, see Covariance#Relationship to inner products, for the columns of  and
and  , correspondingly. The definition of the canonical variables
, correspondingly. The definition of the canonical variables 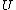 and
and 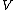 is equivalent to the definition of principal vectors
is equivalent to the definition of principal vectorsPrincipal angles
In linear algebra , the principal angles, also called canonical angles, provide information about the relative position of two subspaces of a Euclidean space...
for the pair of subspaces spanned by the columns of
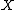 and
and 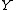 with respect to this inner product. The canonical correlations
with respect to this inner product. The canonical correlations  is equal to the cosine of principal angles
is equal to the cosine of principal anglesPrincipal angles
In linear algebra , the principal angles, also called canonical angles, provide information about the relative position of two subspaces of a Euclidean space...
.
See also
- Regularized canonical correlation analysisRegularized canonical correlation analysisRegularized canonical correlation analysis is a way of using ridge regression to solve the singularity problem in the cross-covariance matrices of canonical correlation analysis...
- Generalized Canonical CorrelationGeneralized canonical correlationIn statistics, the generalized canonical correlation analysis , is a way of making sense of cross-correlation matrices between the sets of random variables when there are more than two sets. While a conventional CCA generalizes Principal component analysis to two sets of random variables, a gCCA ...
- RV coefficientRV coefficientIn statistics, the RV coefficientis a multivariate generalization of the Pearson correlation coefficient.It measures the closeness of two set of points that may each be represented in a matrix....
- Principal anglesPrincipal anglesIn linear algebra , the principal angles, also called canonical angles, provide information about the relative position of two subspaces of a Euclidean space...
External links
- FactoMineR (free exploratory multivariate data analysis software linked to R)
- Understanding canonical correlation analysis (Concepts and Techniques in Modern Geography)
- Canonical correlation analysis — An overview with application to learning methods http://eprints.ecs.soton.ac.uk/9225/01/tech_report03.pdf, pages 5–9 give a good introduction Neural Computation (2004) version
- A note on the ordinal canonical correlation analysis of two sets of ranking scores (Also provides a FORTRAN program)- in J. of Quantitative Economics 7(2), 2009, pp. 173-199
- Representation-Constrained Canonical Correlation Analysis: A Hybridization of Canonical Correlation and Principal Component Analyses (Also provides a FORTRAN program)- in J. of Applied Economic Sciences 4(1), 2009, pp. 115-124

