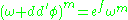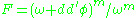Calabi conjecture
Encyclopedia
In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifold
s, made by and proved by .
The Calabi conjecture states that a compact
Kähler manifold
has a unique Kähler metric in the same class whose Ricci form is any given 2-form representing the first Chern class
. In particular if the first Chern class vanishes there is a unique Kähler metric in the same class with vanishing Ricci curvature
; these are called Calabi–Yau manifolds.
The Calabi conjecture is closely related to the question of which Kähler manifolds have Kähler–Einstein metrics.
This was proved for negative first Chern classes independently by Thierry Aubin
and Shing-Tung Yau
in 1976. When the Chern class is zero it was proved by Yau as an easy consequence of the Calabi conjecture.
It was disproved for positive first Chern classes by Yau, who observed that the complex projective plane blown up at 2 points has no Kähler–Einstein metric and so is a counterexample. Also even when Kähler–Einstein metric exists it need not be unique. There has been a lot of further work on the positive first Chern class case. A necessary condition for the existence of a Kähler–Einstein metric is that the Lie algebra of holomorphic vector fields is reductive. Yau conjectured that when the first Chern class is positive, a Kähler variety has a Kähler–Einstein metric if and only if it is stable in the sense of geometric invariant theory
.
The case of complex surfaces has been settled by Gang Tian
. The complex surfaces with positive Chern class are either a product of two copies of a projective line (which obviously has a Kähler–Einstein metric) or a blowup of the projective plane in at most 8 points in "general position", in the sense that no 3 lie on a line and no 6 lie on a quadric. The projective plane has a Kähler–Einstein metric, and the projective plane blown up in 1 or 2 points does not, as the Lie algebra of holomorphic vector fields is not reductive.
Tian showed that the projective plane blown up in 3, 4, 5, 6, 7, or 8 points in general position has a Kähler–Einstein metric.
Yau proved the Calabi conjecture by constructing a solution of this equation using the continuity method. This involves first solving an easier equation, and then showing that a solution to the easy equation can be continuously deformed to a solution of the hard equation. The hardest part of Yau's solution is proving certain a priori estimate
s for the derivatives of solutions.
Any other Kahler form in the same class is of the form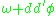
for some smooth function φ on M, unique up to addition of a constant. The Calabi conjecture is therefore equivalent to the following problem:
This is an equation of complex Monge–Ampere type for a single function φ.
It is a particularly hard partial differential equation to solve, as it is non-linear in the terms of highest order.
It is trivial to solve it when f=0, as φ=0 is a solution. The idea of the continuity method is to show that it can be solved for all f by showing that the set of f for which it can be solved is both open and closed. Since the set of f for which it can be solved is non-empty, and the set of all f is connected, this shows that it can be solved for all f.
The map from smooth functions to smooth functions taking φ to F defined by
is neither injective nor surjective. It is not injective because adding a constant to φ does not change F, and it is not surjective
because F must be positive and have average value 1. So we consider the map restricted to functions φ that are normalized to have absolute value 1, and ask if this map is an isomorphism onto the set of positive F=ef with average value 1. Calabi and Yau proved that it is indeed an isomorphism. This is done in several steps, described below.
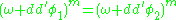
then φ1 and φ2 differ by a constant
(so must be the same if they are both normalized to have average value 0).
Calabi proved this by showing that the average value of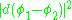
is given by an expression that is at most 0. As it is obviously at least 0, it must be 0, so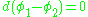
which in turn forces φ1 and φ2 to differ by a constant.
for Banach space
s: in order to apply this, the main step is to show that the linearization of the differential operator above is invertible.
Suppose that F is in the closure of the image of possible
functions φ. This means that there is a sequence of
functions φ1, φ2, ...
such that the corresponding functions F1, F2,...
converge to F, and the problem is to show that some subsequence of the φs converges to a solution φ. In order to do this, Yau finds some a priori bounds for the functions φi and their higher derivatives
in terms of the higher derivatives of log(fi). Finding these bounds requires a long sequence of hard estimates, each improving slightly on the previous estimate. The bounds Yau gets are enough to show that the functions φi all lie in a compact subset of a suitable Banach space of functions, so it is possible to find a convergent subsequence.
This subsequence converges to a function φ with image F, which
shows that the set of possible images F is closed.
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, made by and proved by .
The Calabi conjecture states that a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
has a unique Kähler metric in the same class whose Ricci form is any given 2-form representing the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
. In particular if the first Chern class vanishes there is a unique Kähler metric in the same class with vanishing Ricci curvature
Ricci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
; these are called Calabi–Yau manifolds.
The Calabi conjecture is closely related to the question of which Kähler manifolds have Kähler–Einstein metrics.
Kähler–Einstein metrics
A conjecture closely related to the Calabi conjecture states that if a compact Kähler variety has a negative, zero, or positive first Chern class then it has a Kähler–Einstein metric in the same class as its Kähler metric, unique up to rescaling.This was proved for negative first Chern classes independently by Thierry Aubin
Thierry Aubin
Thierry Aubin was a French mathematician at Centre de Mathématiques de Jussieu who worked on Riemannian geometryand non-linear partial differential equations...
and Shing-Tung Yau
Shing-Tung Yau
Shing-Tung Yau is a Chinese American mathematician working in differential geometry. He was born in Shantou, Guangdong Province, China into a family of scholars from Jiaoling, Guangdong Province....
in 1976. When the Chern class is zero it was proved by Yau as an easy consequence of the Calabi conjecture.
It was disproved for positive first Chern classes by Yau, who observed that the complex projective plane blown up at 2 points has no Kähler–Einstein metric and so is a counterexample. Also even when Kähler–Einstein metric exists it need not be unique. There has been a lot of further work on the positive first Chern class case. A necessary condition for the existence of a Kähler–Einstein metric is that the Lie algebra of holomorphic vector fields is reductive. Yau conjectured that when the first Chern class is positive, a Kähler variety has a Kähler–Einstein metric if and only if it is stable in the sense of geometric invariant theory
Geometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
.
The case of complex surfaces has been settled by Gang Tian
Gang Tian
Tian Gang is a Chinese mathematician and an academician of the Chinese Academy of Sciences. He is known for his contributions to geometric analysis and quantum cohomology, among other fields...
. The complex surfaces with positive Chern class are either a product of two copies of a projective line (which obviously has a Kähler–Einstein metric) or a blowup of the projective plane in at most 8 points in "general position", in the sense that no 3 lie on a line and no 6 lie on a quadric. The projective plane has a Kähler–Einstein metric, and the projective plane blown up in 1 or 2 points does not, as the Lie algebra of holomorphic vector fields is not reductive.
Tian showed that the projective plane blown up in 3, 4, 5, 6, 7, or 8 points in general position has a Kähler–Einstein metric.
Outline of the proof
Calabi transformed the Calabi conjecture into a non–linear partial differential equation of complex Monge–Ampere type, and showed that there is at most one solution.Yau proved the Calabi conjecture by constructing a solution of this equation using the continuity method. This involves first solving an easier equation, and then showing that a solution to the easy equation can be continuously deformed to a solution of the hard equation. The hardest part of Yau's solution is proving certain a priori estimate
A priori estimate
In the theory of partial differential equations, an a priori estimate is an estimate for the size of a solution or its derivatives of a partial differential equation. A priori is Latin for "from before" and refers to the fact that the estimate for the solution is derived before the solution is...
s for the derivatives of solutions.
Transformation of the Calabi conjecture to a differential equation
Suppose that M is a complex compact manifold with a Kahler form ω.Any other Kahler form in the same class is of the form
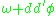
for some smooth function φ on M, unique up to addition of a constant. The Calabi conjecture is therefore equivalent to the following problem:
- Let F=ef be a positive smooth function on M with average value 1. Then there is a smooth real function φ with
- and φ is unique up to addition of a constant.
This is an equation of complex Monge–Ampere type for a single function φ.
It is a particularly hard partial differential equation to solve, as it is non-linear in the terms of highest order.
It is trivial to solve it when f=0, as φ=0 is a solution. The idea of the continuity method is to show that it can be solved for all f by showing that the set of f for which it can be solved is both open and closed. Since the set of f for which it can be solved is non-empty, and the set of all f is connected, this shows that it can be solved for all f.
The map from smooth functions to smooth functions taking φ to F defined by
is neither injective nor surjective. It is not injective because adding a constant to φ does not change F, and it is not surjective
because F must be positive and have average value 1. So we consider the map restricted to functions φ that are normalized to have absolute value 1, and ask if this map is an isomorphism onto the set of positive F=ef with average value 1. Calabi and Yau proved that it is indeed an isomorphism. This is done in several steps, described below.
Uniqueness of the solution
Proving that the solution is unique involves showing that if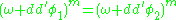
then φ1 and φ2 differ by a constant
(so must be the same if they are both normalized to have average value 0).
Calabi proved this by showing that the average value of
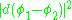
is given by an expression that is at most 0. As it is obviously at least 0, it must be 0, so
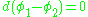
which in turn forces φ1 and φ2 to differ by a constant.
The set of F is open
Proving that the set of possible F is open (in the set of smooth functions with average value 1) involves showing that if it is possible to solve the equation for some F, then it is possible to solve it for all sufficiently close F. Calabi proved this by using the implicit function theoremImplicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
for Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s: in order to apply this, the main step is to show that the linearization of the differential operator above is invertible.
The set of F is closed
This is the hardest part of the proof, and was the part done by Yau.Suppose that F is in the closure of the image of possible
functions φ. This means that there is a sequence of
functions φ1, φ2, ...
such that the corresponding functions F1, F2,...
converge to F, and the problem is to show that some subsequence of the φs converges to a solution φ. In order to do this, Yau finds some a priori bounds for the functions φi and their higher derivatives
in terms of the higher derivatives of log(fi). Finding these bounds requires a long sequence of hard estimates, each improving slightly on the previous estimate. The bounds Yau gets are enough to show that the functions φi all lie in a compact subset of a suitable Banach space of functions, so it is possible to find a convergent subsequence.
This subsequence converges to a function φ with image F, which
shows that the set of possible images F is closed.