
CIR process
Encyclopedia
The CIR process is a Markov process
with continuous paths defined by the following stochastic differential equation
(SDE):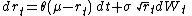
where Wt is a standard Wiener process
and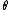 ,
, 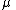 and
and  are the parameter
are the parameter
s. The parameter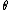 corresponds to the speed of adjustment,
corresponds to the speed of adjustment, 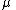 to the mean and
to the mean and 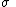 to volatility.
to volatility.
This process can be defined as a sum of squared Ornstein–Uhlenbeck process. The CIR is an ergodic process, and possesses a stationary distribution, which is a gamma.
This process is widely used in finance
to model short term interest rate
(see Cox–Ingersoll–Ross model). It is also used to model stochastic volatility
in the Heston model
.
Given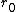 and defining
and defining 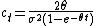 ,
, 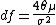 and
and 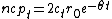 , it can be shown that
, it can be shown that 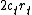 follows a noncentral chi-squared distribution with degree of freedom
follows a noncentral chi-squared distribution with degree of freedom 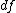 and non-centrality parameter
and non-centrality parameter 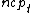 . Note that
. Note that 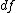 is constant.
is constant.
Provided that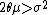 , the process has a stationary gamma distribution with shape parameter
, the process has a stationary gamma distribution with shape parameter 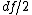 and scale parameter
and scale parameter 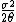 .
.
The continuous SDE can be discretized as follows
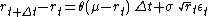 ,
,
which is equivalent to
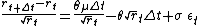 .This equation can be used for a linear regression.
.This equation can be used for a linear regression.
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
with continuous paths defined by the following stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
(SDE):
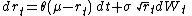
where Wt is a standard Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and
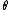 ,
, 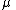 and
and  are the parameter
are the parameterParameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s. The parameter
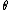 corresponds to the speed of adjustment,
corresponds to the speed of adjustment, 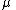 to the mean and
to the mean and 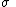 to volatility.
to volatility.This process can be defined as a sum of squared Ornstein–Uhlenbeck process. The CIR is an ergodic process, and possesses a stationary distribution, which is a gamma.
This process is widely used in finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
to model short term interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
(see Cox–Ingersoll–Ross model). It is also used to model stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
in the Heston model
Heston model
In finance, the Heston model, named after Steven Heston, is a mathematical model describing the evolution of the volatility of an underlying asset...
.
Distribution
- Conditional distribution
Given
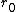 and defining
and defining 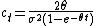 ,
, 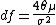 and
and 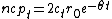 , it can be shown that
, it can be shown that 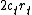 follows a noncentral chi-squared distribution with degree of freedom
follows a noncentral chi-squared distribution with degree of freedom 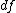 and non-centrality parameter
and non-centrality parameter 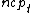 . Note that
. Note that 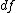 is constant.
is constant.- Stationary distribution
Provided that
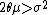 , the process has a stationary gamma distribution with shape parameter
, the process has a stationary gamma distribution with shape parameter 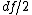 and scale parameter
and scale parameter 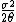 .
.Properties
- Mean reversionMean reversionMean reversion is a mathematical concept sometimes used for stock investing, but it can be applied to other assets. In general terms, the essence of the concept is the assumption that both a stock's high and low prices are temporary and that a stock's price will tend to move to the average price...
, - Level dependent volatility (
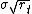 ),
), - For given positive
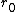 the process will never touch zero, if
the process will never touch zero, if 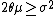 ; otherwise it can occasionally touch the zero point,
; otherwise it can occasionally touch the zero point, 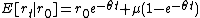 , so long term mean is
, so long term mean is 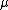 ,
, .
.
Calibration
- Ordinary least squaresOrdinary least squaresIn statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
The continuous SDE can be discretized as follows
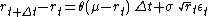 ,
,which is equivalent to
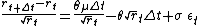 .This equation can be used for a linear regression.
.This equation can be used for a linear regression.- Martingale estimation
- Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....

