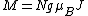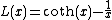
Brillouin function
Encyclopedia
Brillouin Function
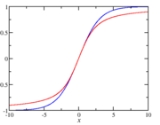
The Brillouin function is a special function defined by the following equation:The function is usually applied (see below) in the context where x is a real variable and J is a positive integer or half-integer. In this case, the function varies from -1 to 1, approaching +1 as
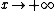 and -1 as
and -1 as  .
.The function is best known for arising in the calculation of the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
of an ideal paramagnet. In particular, it describes the dependency of the magnetization
 on the applied magnetic field
on the applied magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
 and the total angular momentum quantum number J of the microscopic magnetic moment
and the total angular momentum quantum number J of the microscopic magnetic momentMagnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
s of the material. The magnetization is given by:
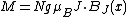
where
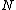 is the number of atoms per unit volume,
is the number of atoms per unit volume, the g-factor,
the g-factor, the Bohr magneton,
the Bohr magneton, is the ratio of the ZeemanZeeman effectThe Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
is the ratio of the ZeemanZeeman effectThe Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
energy of the magnetic moment in the external field to the thermal energy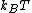 :
:
-
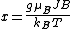
 is the Boltzmann constant and
is the Boltzmann constant and  the temperature.
the temperature.
| Click "show" to see a derivation of this law: |
|---|
| A derivation of this law describing the magnetization of an ideal paramagnet is as follows. Let z be the direction of the magnetic field. The z-component of the angular momentum of each magnetic moment (a.k.a. the azimuthal quantum number Azimuthal quantum number The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital... ) can take on one of the 2J+1 possible values -J,-J+1,...,+J. Each of these has a different energy, due to the external field B: The energy associated with quantum number m is  (where g is the g-factor, μB is the Bohr magneton, and x is as defined in the text above). The relative probability of each of these is given by the Boltzmann factor Boltzmann factor In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T... : 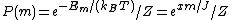 where Z (the partition function Partition function (statistical mechanics) Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas... ) is a normalization constant such that the probabilities sum to unity. Calculating Z, the result is: 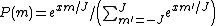 . .All told, the expectation value of the azimuthal quantum number m is 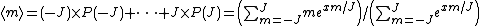 . .The denominator is a geometric series and the numerator is a type of arithmetic-geometric series, so the series can be explicitly summed. After some algebra, the result turns out to be  With N magnetic moments per unit volume, the magnetization density is 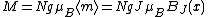 . . |
Langevin Function

 can assume all values (
can assume all values (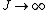 ). The Brillouin function is then simplified into the Langevin function, named after Paul Langevin
). The Brillouin function is then simplified into the Langevin function, named after Paul LangevinPaul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
:
For small values of , the Langevin function can be approximated by a truncation of its Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
:
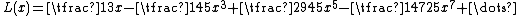
An alternative better behaved approximation can be derived from the
Lambert's continued fraction expansion of :
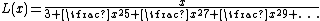
For small enough , both approximations are numerically better than a direct evaluation of the actual analytical expression, since the later suffers from Loss of significance
Loss of significance
Loss of significance is an undesirable effect in calculations using floating-point arithmetic. It occurs when an operation on two numbers increases relative error substantially more than it increases absolute error, for example in subtracting two large and nearly equal numbers. The effect is that...
.
The inverse Langevin function can be approximated to within 5% accuracy
by the formula
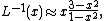
valid on the whole interval (-1, 1).
For small values of x, better approximations are the Padé approximant
Padé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....

and the
Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

High Temperature Limit
When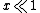 i.e. when
i.e. when  is small, the expression of the magnetization can be approximated by the Curie's law
is small, the expression of the magnetization can be approximated by the Curie's lawCurie's law
In a paramagnetic material the magnetization of the material is directly proportional to an applied magnetic field. However, if the material is heated, this proportionality is reduced: for a fixed value of the field, the magnetization is inversely proportional to temperature...
:
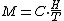
where
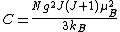 is a constant. One can note that
is a constant. One can note that 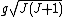 is the effective number of Bohr magnetons.
is the effective number of Bohr magnetons.High Field Limit
When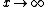 , the Brillouin function goes to 1. The magnetization saturates with the magnetic moments completely aligned with the applied field:
, the Brillouin function goes to 1. The magnetization saturates with the magnetic moments completely aligned with the applied field: