
Kleene–Brouwer order
Encyclopedia
In descriptive set theory
, the Kleene–Brouwer order is a linear order on finite sequences of some linearly ordered set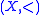 . Note that such a set of finite sequences can be viewed as a tree on
. Note that such a set of finite sequences can be viewed as a tree on  , thus the Kleene-Brouwer order is a natural linear ordering that can be put on a tree.
, thus the Kleene-Brouwer order is a natural linear ordering that can be put on a tree.
If and
and  are finite sequences of elements from
are finite sequences of elements from  , we say that
, we say that  when there is an
when there is an  such that either:
such that either:
In simple terms, whenever
whenever  is longer (ie. if
is longer (ie. if  terminates before
terminates before  ) or
) or  is to the "left" of
is to the "left" of  on the first place they differ.
on the first place they differ.
Its importance comes from the fact that if is well-ordered, then a tree over
is well-ordered, then a tree over  is well-founded
is well-founded
if and only if the Kleene–Brouwer ordering is a well-ordering of the elements of the tree.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, the Kleene–Brouwer order is a linear order on finite sequences of some linearly ordered set
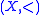 . Note that such a set of finite sequences can be viewed as a tree on
. Note that such a set of finite sequences can be viewed as a tree on  , thus the Kleene-Brouwer order is a natural linear ordering that can be put on a tree.
, thus the Kleene-Brouwer order is a natural linear ordering that can be put on a tree.If
 and
and  are finite sequences of elements from
are finite sequences of elements from  , we say that
, we say that  when there is an
when there is an  such that either:
such that either:
-
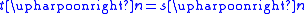 and
and 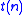 is defined but
is defined but 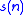 is undefined (ie.
is undefined (ie.  properly extends
properly extends  ), or
), or - both
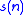 and
and 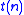 are defined,
are defined,  , and
, and 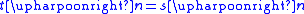 .
.
In simple terms,
 whenever
whenever  is longer (ie. if
is longer (ie. if  terminates before
terminates before  ) or
) or  is to the "left" of
is to the "left" of  on the first place they differ.
on the first place they differ.Its importance comes from the fact that if
 is well-ordered, then a tree over
is well-ordered, then a tree over  is well-founded
is well-foundedWell-founded relation
In mathematics, a binary relation, R, is well-founded on a class X if and only if every non-empty subset of X has a minimal element with respect to R; that is, for every non-empty subset S of X, there is an element m of S such that for every element s of S, the pair is not in R:\forall S...
if and only if the Kleene–Brouwer ordering is a well-ordering of the elements of the tree.

