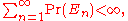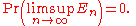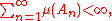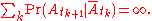Borel-Cantelli lemma
Encyclopedia
In probability theory
, the Borel–Cantelli lemma is a theorem
about sequence
s of events
. In general, it is a result in measure theory. It is named after Émile Borel
and Francesco Paolo Cantelli
. A related result, sometimes called the second Borel–Cantelli lemma, is a partial converse of the first Borel–Cantelli lemma.
.
The Borel–Cantelli lemma states:
Here, "lim sup" denotes limit superior of the sequence of events, and each event is a set of outcomes. That is, lim sup En is the set of outcomes that occur infinitely many times within the infinite sequence of events (En). Explicitly,
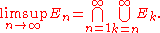
The theorem therefore asserts that if the sum of the probabilities of the events En is finite, then the set of all outcomes that are "repeated" infinitely many times must occur with probability zero. Note that no assumption of independence
is required.
Suppose (Xn) is a sequence of random variable
s with Pr(Xn = 0) = 1/n2 for each n. The probability that Xn = 0 occurs for infinitely many n is equivalent to the probability of the intersection of infinitely many [Xn = 0] events. The intersection of infinitely many such events is a set of outcomes common to all of them. However, the sum ∑Pr(Xn = 0) converges to π2/6 ≈ 1.645 < ∞, and so the Borel–Cantelli Lemma states that the set of outcomes that are common to infinitely many such events occurs with probability zero. Hence, the probability of Xn = 0 occurring for infinitely many n is 0. Almost surely
(i.e., with probability 1), Xn is nonzero for all but finitely many n.
and suppose that the sum of the probabilities of the En is finite. That is suppose:
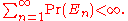
Note that the convergence of this sum implies:
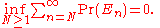
Therefore it follows that:
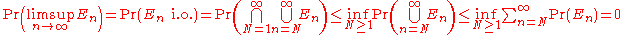
where the abbreviation "i.o." denotes "infinitely often."
and the sum of the probabilities of the En diverges to infinity, then the probability that infinitely many of them occur is 1. That is:
The assumption of independence can be weakened to pairwise independence
, but in that case the proof is more difficult.
is a special case of this lemma.
The lemma can be applied to give a covering theorem in Rn. Specifically , if Ej is a collection of Lebesgue measurable
subsets of a compact set in Rn such that
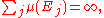
then there is a sequence Fj of translates
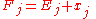
such that
apart from a set of measure zero.
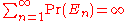and the events 
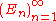are independent. It is sufficient to show the event that the En's did not occur for infinitely many values of n has probability 0. This is just to say that it is sufficient to show that
Noting that:
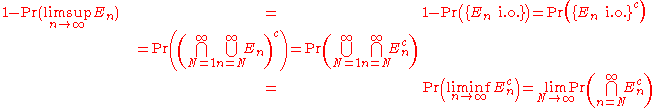
it is enough to show: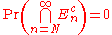
. Since the 
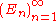are independent:
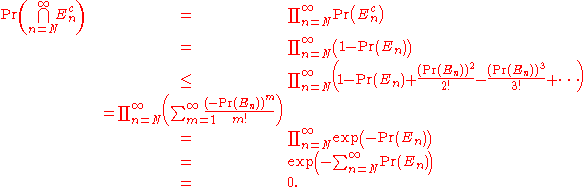
This completes the proof. Alternatively, we can see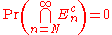
by taking negative the logarithm of both sides to get:
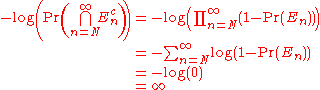
Since −log(1 − x) ≥ x for all x > 0, the result similarly follows from our assumption that
Lemma in the sense that it gives a necessary and sufficient condition for the limsup to be 1 by replacing the independence assumption by the completely different assumption that
is monotone increasing for sufficiently large indices. This Lemma says:
Let
be such that 
,
and let
denote the complement of 
. Then the probability of infinitely many 
occur (that is, at least one 
occurs) is one if and only if there exists a strictly increasing sequence of positive integers 
such that
This simple result can be useful in problems such as for instance those involving hitting probabilities for stochastic process
with the choice of the sequence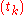
usually being the essence.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Borel–Cantelli lemma is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of events
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
. In general, it is a result in measure theory. It is named after Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
and Francesco Paolo Cantelli
Francesco Paolo Cantelli
Francesco Paolo Cantelli was an Italian mathematician. He was the founder of the Istituto Italiano degli Attuari for the applications of mathematics and probability to economics....
. A related result, sometimes called the second Borel–Cantelli lemma, is a partial converse of the first Borel–Cantelli lemma.
Statement of lemma for probability spaces
Let (En) be a sequence of events in some probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
.
The Borel–Cantelli lemma states:
- If the sum of the probabilities of the En is finite
- then the probability that infinitely many of them occur is 0, that is,
Here, "lim sup" denotes limit superior of the sequence of events, and each event is a set of outcomes. That is, lim sup En is the set of outcomes that occur infinitely many times within the infinite sequence of events (En). Explicitly,
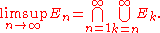
The theorem therefore asserts that if the sum of the probabilities of the events En is finite, then the set of all outcomes that are "repeated" infinitely many times must occur with probability zero. Note that no assumption of independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
is required.
Example
Suppose (Xn) is a sequence of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with Pr(Xn = 0) = 1/n2 for each n. The probability that Xn = 0 occurs for infinitely many n is equivalent to the probability of the intersection of infinitely many [Xn = 0] events. The intersection of infinitely many such events is a set of outcomes common to all of them. However, the sum ∑Pr(Xn = 0) converges to π2/6 ≈ 1.645 < ∞, and so the Borel–Cantelli Lemma states that the set of outcomes that are common to infinitely many such events occurs with probability zero. Hence, the probability of Xn = 0 occurring for infinitely many n is 0. Almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
(i.e., with probability 1), Xn is nonzero for all but finitely many n.
Proof
Let (En) be a sequence of events in some probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
and suppose that the sum of the probabilities of the En is finite. That is suppose:
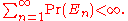
Note that the convergence of this sum implies:
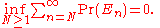
Therefore it follows that:
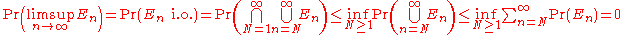
where the abbreviation "i.o." denotes "infinitely often."
General measure spaces
For general measure spaces, the Borel–Cantelli lemma takes the following form:- Let μ be a (positive) measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a set X, with σ-algebraSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
F, and let (An) be a sequence in F. If
- then
Converse result
A related result, sometimes called the second Borel–Cantelli lemma, is a partial converse of the first Borel–Cantelli lemma. The lemma states: If the events En are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
and the sum of the probabilities of the En diverges to infinity, then the probability that infinitely many of them occur is 1. That is:
-
- If
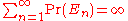and the events 
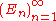are independent, then 
- If
The assumption of independence can be weakened to pairwise independence
Pairwise independence
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent...
, but in that case the proof is more difficult.
Example
The infinite monkey theoremInfinite monkey theorem
The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare....
is a special case of this lemma.
The lemma can be applied to give a covering theorem in Rn. Specifically , if Ej is a collection of Lebesgue measurable
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
subsets of a compact set in Rn such that
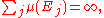
then there is a sequence Fj of translates
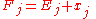
such that
apart from a set of measure zero.
Proof
Suppose that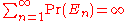 and the events 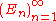are independent. It is sufficient to show the event that the En's did not occur for infinitely many values of n has probability 0. This is just to say that it is sufficient to show that
Noting that:
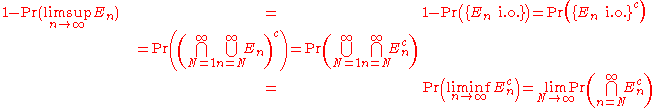
it is enough to show:
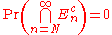. Since the 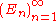are independent: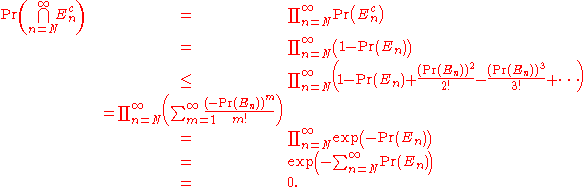This completes the proof. Alternatively, we can see
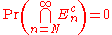by taking negative the logarithm of both sides to get: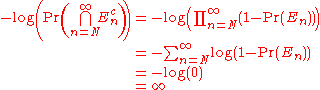Since −log(1 − x) ≥ x for all x > 0, the result similarly follows from our assumption that
Counterpart
Another related result is the so-called counterpart of the Borel–Cantelli lemma. It is a counterpart of theLemma in the sense that it gives a necessary and sufficient condition for the limsup to be 1 by replacing the independence assumption by the completely different assumption that
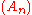is monotone increasing for sufficiently large indices. This Lemma says:Let
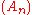be such that ,and let
denote the complement of . Then the probability of infinitely many occur (that is, at least one occurs) is one if and only if there exists a strictly increasing sequence of positive integers such that
This simple result can be useful in problems such as for instance those involving hitting probabilities for stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with the choice of the sequence
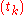usually being the essence.External links
- Planet Math Proof Refer for a simple proof of the Borel Cantelli Lemma