Bogacki–Shampine method
Encyclopedia
The Bogacki–Shampine method is a method for the numerical solution of ordinary differential equations
, that was proposed by Przemyslaw Bogacki and Lawrence F. Shampine in 1989 . The Bogacki–Shampine method is a Runge–Kutta method of order three with four stages with the First Same As Last (FSAL) property, so that it uses approximately three function evaluations per step. It has an embedded second-order method which can be used to implement adaptive step size. The Bogacki–Shampine method is implemented in the
.
Low-order methods are more suitable than higher-order methods like the Dormand–Prince method
of order five, if only a crude approximation to the solution is required. Bogacki and Shampine argue that their method outperforms other third-order methods with an embedded method of order two.
The Butcher tableau for the Bogacki–Shampine method is:
Following the standard notation, the differential equation to be solved is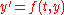
. Furthermore, 
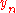denotes the numerical solution at time 
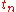and 
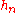is the step size, defined by 
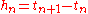. Then, one step of the Bogacki–Shampine method is given by:
Here,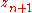
is a third-order approximation to the exact solution. The method for calculating 
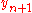is due to . On the other hand, 
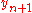is a second-order approximation, so the difference between 
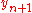and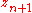 
can be used to adapt the step size
. The FSAL property is that the stage value
in one step equals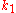 
in the next step; thus, only three function evaluations are needed per step.
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
, that was proposed by Przemyslaw Bogacki and Lawrence F. Shampine in 1989 . The Bogacki–Shampine method is a Runge–Kutta method of order three with four stages with the First Same As Last (FSAL) property, so that it uses approximately three function evaluations per step. It has an embedded second-order method which can be used to implement adaptive step size. The Bogacki–Shampine method is implemented in the
ode23 function in MATLABMATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
.
Low-order methods are more suitable than higher-order methods like the Dormand–Prince method
Dormand–Prince method
In numerical analysis, the Dormand–Prince method, or DOPRI method, is a method for solving ordinary differential equations . The method is a member of the Runge–Kutta family of ODE solvers. More specifically, it uses six function evaluations to calculate fourth- and fifth-order accurate solutions...
of order five, if only a crude approximation to the solution is required. Bogacki and Shampine argue that their method outperforms other third-order methods with an embedded method of order two.
The Butcher tableau for the Bogacki–Shampine method is:
| 0 | ||||
| | 1/2 | 1/2 | |||
| | 3/4 | 0 | 3/4 | ||
| | 1 | 2/9 | 1/3 | 4/9 | |
| | | 2/9 | 1/3 | 4/9 | 0 |
| | | 7/24 | 1/4 | 1/3 | 1/8 |
Following the standard notation, the differential equation to be solved is
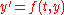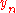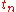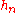. Furthermore, denotes the numerical solution at time and is the step size, defined by 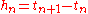. Then, one step of the Bogacki–Shampine method is given by:Here,
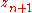is a third-order approximation to the exact solution. The method for calculating 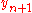is due to . On the other hand, 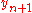is a second-order approximation, so the difference between 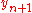and 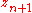can be used to adapt the step sizeAdaptive stepsize
Adaptive stepsize is a technique in numerical analysis used for many problems, but mainly for integration. It can be used for both normal integration , or the process of solving an ordinary differential equation. This article focuses on the latter...
. The FSAL property is that the stage value
in one step equals 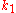in the next step; thus, only three function evaluations are needed per step.