
Bochner's formula
Encyclopedia
In mathematics
, Bochner's formula is a statement relating harmonic functions on a Riemannian manifold
 to the Ricci curvature
to the Ricci curvature
. More specifically, if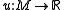 is a harmonic function (i.e.,
is a harmonic function (i.e., 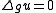 , where
, where  is the Laplacian
is the Laplacian
with respect to ), then
), then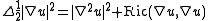 ,
,
where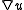 is the gradient
is the gradient
of with respect to
with respect to  . Bochner used this formula to prove the Bochner vanishing theorem.
. Bochner used this formula to prove the Bochner vanishing theorem.
The Bochner formula is often proved using supersymmetry
or Clifford algebra
methods.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Bochner's formula is a statement relating harmonic functions on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
 to the Ricci curvature
to the Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
. More specifically, if
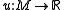 is a harmonic function (i.e.,
is a harmonic function (i.e., 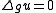 , where
, where  is the Laplacian
is the LaplacianLaplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
with respect to
 ), then
), then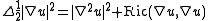 ,
,where
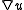 is the gradient
is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
 with respect to
with respect to  . Bochner used this formula to prove the Bochner vanishing theorem.
. Bochner used this formula to prove the Bochner vanishing theorem.The Bochner formula is often proved using supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
or Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
methods.

