Birkhoff polytope
Encyclopedia
The Birkhoff polytope Bn, also called the assignment polytope, the polytope of doubly stochastic matrices, or the perfect matching polytope of the complete bipartite graph
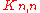, is the convex polytope
in RN (where N = n²) whose points are the doubly stochastic matrices
, i.e., the matrices whose entries are non-negative real numbers and whose rows and columns each add up to 1.
s of the Birkhoff polytope are the permutation matrices, and therefore that any doubly stochastic matrix may be represented as a convex combination of permutation matrices; this was stated in a 1946 paper by Garrett Birkhoff
, but equivalent results in the languages of projective configurations and of regular
bipartite graph
matchings, respectively, were shown much earlier in 1894 in Ernst Steinitz
's thesis and in 1916 by Dénes Kőnig
.
Therefore, the Birkhoff polytope has n! vertices, one for each permutation on n items.
that the sum of each row and of each column be one. Within this subspace, it is defined by n2 linear inequalities
, one for each coordinate of the matrix, specifying that the coordinate be non-negative.
Therefore, it has exactly n2 facets.
and face-transitive (i.e. the dual polytope
is vertex-transitive). It is not regular
for n>2.
x. A combinatorial formula for all n was given in 2007. The following asymptotic formula
was found by
Rodney Canfield and Brendan McKay
:
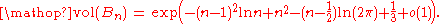
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
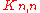, is the convex polytopeConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
in RN (where N = n²) whose points are the doubly stochastic matrices
Doubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
, i.e., the matrices whose entries are non-negative real numbers and whose rows and columns each add up to 1.
Vertices
The Birkhoff–von Neumann theorem states that the extreme pointExtreme point
In mathematics, an extreme point of a convex set S in a real vector space is a point in S which does not lie in any open line segment joining two points of S...
s of the Birkhoff polytope are the permutation matrices, and therefore that any doubly stochastic matrix may be represented as a convex combination of permutation matrices; this was stated in a 1946 paper by Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
, but equivalent results in the languages of projective configurations and of regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
matchings, respectively, were shown much earlier in 1894 in Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
's thesis and in 1916 by Dénes Kőnig
Dénes König
Dénes Kőnig was a Jewish Hungarian mathematician who worked in and wrote the first textbook on the field of graph theory....
.
Therefore, the Birkhoff polytope has n! vertices, one for each permutation on n items.
Facets
The Birkhoff polytope lies within an dimensional affine subspace of the n2-dimensional space of all matrices: this subspace is determined by the linear equality constraintsthat the sum of each row and of each column be one. Within this subspace, it is defined by n2 linear inequalities
Linear inequality
In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....
, one for each coordinate of the matrix, specifying that the coordinate be non-negative.
Therefore, it has exactly n2 facets.
Symmetries
Bikrkhoff polytope Bn is both vertex-transitiveVertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and face-transitive (i.e. the dual polytope
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
is vertex-transitive). It is not regular
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
for n>2.
Volume
An outstanding problem is to find the volume of the Birkhoff polytopes. This has been done for n ≤ 10. It is known to be equal to the volume of a polytope associated with standard Young tableauYoung tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x. A combinatorial formula for all n was given in 2007. The following asymptotic formula
Asymptotic formula
In mathematics, an asymptotic formula for a quantity depending on natural numbers, or on a variable taking real numbers as values, is a function of natural numbers, or of a real variable, whose values are nearly equal to the values of the former when both are evaluated for the same large values...
was found by
Rodney Canfield and Brendan McKay
Brendan McKay
Brendan Damien McKay is a Professor in the Research School of Computer Science at the Australian National University . He has published extensively in combinatorics....
:
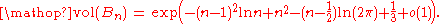
Generalizations
- The Birkhoff polytope is a special case of the transportation polytope, a polytope of nonnegative rectangular matrices with given row and column sums. The integer points in these polytopes are called contingency tableContingency tableIn statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
s; they play an important role in Bayesian statisticsBayesian statisticsBayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
. - The Birkhoff polytope is a special case of the matching polytope, defined as a convex hull of the perfect matchings in a finite graph. The description of facets in this generality was given by Jack EdmondsJack EdmondsJack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
(1965), and is related to Edmonds's matching algorithmEdmonds's matching algorithmEdmonds's matching algorithmis an algorithm in graph theory for constructing maximum matchings on graphs. The algorithm was discovered by Jack Edmonds in 1965. Given a general graph G = , the algorithm finds a matching M such that each vertex in V is incident with at most one edge in M and |M| is...
.
Additional reading
- Matthias Beck and Dennis Pixton (2003), The Ehrhart polynomial of the Birkhoff polytope, Discrete and Computational GeometryDiscrete and Computational GeometryDiscrete & Computational Geometry is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986, the journal publishes articles on in discrete geometry and computational geometry....
, Vol. 30, pp. 623–637. The volume of B9.
External links
- Birkhoff polytope Web site by Dennis Pixton and Matthias Beck, with links to articles and volumes.