
Bicircular matroid
Encyclopedia
In the mathematical
subject of matroid
theory, the bicircular matroid of a graph
G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforest
s of G, that is, the edge sets in which each connected component
contains at most one cycle
. The circuits, or minimal dependent sets, of this matroid are the bicircular graphs (or bicycles, but that term has other meanings in graph theory); these are the theta graph, consisting of three paths joining the same two vertices but not intersecting each other, the figure eight graph (or tight handcuff), which consists of two cycles having just one common vertex, and the loose handcuff (or barbell), which consists of two disjoint cycles and a minimal connecting path. All these definitions apply to multigraph
s, i.e., they permit multiple edges (edges sharing the same endpoints) and loops (edges whose two endpoints are the same vertex).
The bicircular matroid was introduced by Simões-Pereira and explored further by Matthews and others. It is a special case of the frame matroid of a biased graph
.
Bicircular matroids can be characterized as the transversal matroids that arise when no point belongs to more than two sets. A transversal presentation in terms of a point set and a class of subsets comes directly from the graph. The points of the presentation are the edges. There is one set for each vertex, and it consists of the edges which have that vertex as an endpoint.
The closed sets (flats) of the bicircular matroid of a graph G can be described as the forest
s F of G such that in the induced subgraph in V(G) − V(F), every connected component has a cycle. Since the flats of a matroid form a geometric lattice when partially ordered by set inclusion, these forests of G also form a geometric lattice. Their partial ordering is that F1 ≤ F2 if
For the most interesting example, let G o be G with a loop added to every vertex. Then the flats of B(G o) are all forests of G, spanning or nonspanning; thus, all forests of a graph G form a geometric lattice, the forest lattice of G (Zaslavsky 1982).
Unlike transversal matroids in general, bicircular matroids form a minor-closed class; that is, any submatroid or contraction of a bicircular matroid is also a bicircular matroid. (That can be seen from their description in terms of biased graph
s (Zaslavsky 1991).)
Here is a description of deletion and contraction of an edge in terms of the underlying graph: To delete an edge from the matroid, remove it from the graph. The rule for contraction depends on what kind of edge it is. To contract a link (a non-loop) in the matroid, contract it in the graph in the usual way. To contract a loop e at vertex v, delete e and v but not the other edges incident with v; rather, each edge incident with v and another vertex w becomes a loop at w. Any other graph loops at v become matroid loops—to describe this correctly in terms of the graph one needs half-edges and loose edges; see biased graph minors.
s (forests that contain all vertices of G) of each size in G. The formula is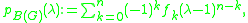
where fk equals the number of k-edge spanning forests in G. See Zaslavsky (1982).
. However, they cannot be represented by vectors over an arbitrary finite field
. The question of the fields over which a bicircular matroid has a vector representation leads to the largely unsolved problem of finding the fields over which a graph has multiplicative gains
. See Zaslavsky (2007).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subject of matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
theory, the bicircular matroid of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
G is the matroid B(G) whose points are the edges of G and whose independent sets are the edge sets of pseudoforest
Pseudoforest
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...
s of G, that is, the edge sets in which each connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
contains at most one cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
. The circuits, or minimal dependent sets, of this matroid are the bicircular graphs (or bicycles, but that term has other meanings in graph theory); these are the theta graph, consisting of three paths joining the same two vertices but not intersecting each other, the figure eight graph (or tight handcuff), which consists of two cycles having just one common vertex, and the loose handcuff (or barbell), which consists of two disjoint cycles and a minimal connecting path. All these definitions apply to multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s, i.e., they permit multiple edges (edges sharing the same endpoints) and loops (edges whose two endpoints are the same vertex).
The bicircular matroid was introduced by Simões-Pereira and explored further by Matthews and others. It is a special case of the frame matroid of a biased graph
Biased graph
In mathematics, a biased graph is a graph with a list of distinguished circles , such that if two circles in the list are contained in a theta graph, then so is the third circle of the theta graph...
.
Bicircular matroids can be characterized as the transversal matroids that arise when no point belongs to more than two sets. A transversal presentation in terms of a point set and a class of subsets comes directly from the graph. The points of the presentation are the edges. There is one set for each vertex, and it consists of the edges which have that vertex as an endpoint.
The closed sets (flats) of the bicircular matroid of a graph G can be described as the forest
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
s F of G such that in the induced subgraph in V(G) − V(F), every connected component has a cycle. Since the flats of a matroid form a geometric lattice when partially ordered by set inclusion, these forests of G also form a geometric lattice. Their partial ordering is that F1 ≤ F2 if
- each component tree of F1 is either contained in or vertex-disjoint from every tree of F2 and
- each vertex of F2 is a vertex of F1.
For the most interesting example, let G o be G with a loop added to every vertex. Then the flats of B(G o) are all forests of G, spanning or nonspanning; thus, all forests of a graph G form a geometric lattice, the forest lattice of G (Zaslavsky 1982).
Unlike transversal matroids in general, bicircular matroids form a minor-closed class; that is, any submatroid or contraction of a bicircular matroid is also a bicircular matroid. (That can be seen from their description in terms of biased graph
Biased graph
In mathematics, a biased graph is a graph with a list of distinguished circles , such that if two circles in the list are contained in a theta graph, then so is the third circle of the theta graph...
s (Zaslavsky 1991).)
Here is a description of deletion and contraction of an edge in terms of the underlying graph: To delete an edge from the matroid, remove it from the graph. The rule for contraction depends on what kind of edge it is. To contract a link (a non-loop) in the matroid, contract it in the graph in the usual way. To contract a loop e at vertex v, delete e and v but not the other edges incident with v; rather, each edge incident with v and another vertex w becomes a loop at w. Any other graph loops at v become matroid loops—to describe this correctly in terms of the graph one needs half-edges and loose edges; see biased graph minors.
Characteristic polynomial
The characteristic polynomial of the bicircular matroid B(G o) expresses in a simple way the numbers of spanning forestTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s (forests that contain all vertices of G) of each size in G. The formula is
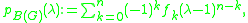
where fk equals the number of k-edge spanning forests in G. See Zaslavsky (1982).
Vector representation
Bicircular matroids, like all other transversal matroids, can be represented by vectors over any infinite fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. However, they cannot be represented by vectors over an arbitrary finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. The question of the fields over which a bicircular matroid has a vector representation leads to the largely unsolved problem of finding the fields over which a graph has multiplicative gains
Gain graph
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
. See Zaslavsky (2007).

