Bessel process
Encyclopedia
In mathematics
, a Bessel process, named after Friedrich Bessel
, is a type of stochastic process
. The n-dimension
al Bessel process is the real-valued
process X given by
where ||·|| denotes the Euclidean norm in Rn and W is an n-dimensional Wiener process
(Brownian motion
) started from the origin.
The n-dimensional Bessel process is the solution to the stochastic differential equation
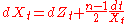
where Z is a 1-dimensional Wiener process
(Brownian motion
). Note that this SDE makes sense for any real parameter
(although the drift term is singular at zero). Since W was assumed to have started from the origin the initial condition is X0 = 0.
For n ≥ 2, the n-dimensional Wiener process is transient from its starting point: with probability one
, Xt > 0 for all t > 0. It is, however, neighbourhood-recurrent for n = 2, meaning that with probability 1, for any r > 0, there are arbitrarily large t with Xt < r; on the other hand, it is truly transient for n > 2, meaning that Xt ≥ r for all t sufficiently large.
A notation for the n-dimensional Bessel process started at zero is BES0(n).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Bessel process, named after Friedrich Bessel
Friedrich Bessel
-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...
, is a type of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. The n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Bessel process is the real-valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
process X given by
where ||·|| denotes the Euclidean norm in Rn and W is an n-dimensional Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) started from the origin.
The n-dimensional Bessel process is the solution to the stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
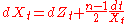
where Z is a 1-dimensional Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
). Note that this SDE makes sense for any real parameter
(although the drift term is singular at zero). Since W was assumed to have started from the origin the initial condition is X0 = 0.For n ≥ 2, the n-dimensional Wiener process is transient from its starting point: with probability one
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
, Xt > 0 for all t > 0. It is, however, neighbourhood-recurrent for n = 2, meaning that with probability 1, for any r > 0, there are arbitrarily large t with Xt < r; on the other hand, it is truly transient for n > 2, meaning that Xt ≥ r for all t sufficiently large.
A notation for the n-dimensional Bessel process started at zero is BES0(n).