
Belyi's theorem
Encyclopedia
In mathematics
, Belyi's theorem on algebraic curve
s states that any non-singular algebraic curve C, defined by algebraic number
coefficients, represents a compact Riemann surface
which is a ramified covering of the Riemann sphere
, ramified at three points only.
It follows that the Riemann surface in question can be taken to be
with H the upper half-plane and Γ of finite index in the modular group
, compactified by cusp
s. Since the modular group has non-congruence subgroups, it is not the conclusion that any such curve is a modular curve
.
This is a result of G. V. Belyi from 1979; it was at that time considered surprising.
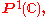
the complex projective line, ramified only over three points - customarily taken to be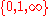 . Belyi functions may be described combinatorially by dessins d'enfants.
. Belyi functions may be described combinatorially by dessins d'enfants.
Belyi functions and dessins d'enfants – but not Belyi's theorem – date at least to the work of Felix Klein
; he used them in his to study an 11-fold cover of the complex projective line with monodromy group PSL(2,11).
for Belyi functions, and has subsequently been much used in the inverse Galois problem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Belyi's theorem on algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s states that any non-singular algebraic curve C, defined by algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
coefficients, represents a compact Riemann surface
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
which is a ramified covering of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, ramified at three points only.
It follows that the Riemann surface in question can be taken to be
- H/Γ
with H the upper half-plane and Γ of finite index in the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, compactified by cusp
Cusp
Cusp may refer to:*Beach cusps, a pointed and regular arc pattern of the shoreline at the beach*Behavioral cusp an important behavior change with far reaching consequences*Cusp catastrophe...
s. Since the modular group has non-congruence subgroups, it is not the conclusion that any such curve is a modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
.
This is a result of G. V. Belyi from 1979; it was at that time considered surprising.
Belyi functions
A Belyi function is a holomorphic map from a compact Riemann surface to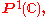
the complex projective line, ramified only over three points - customarily taken to be
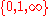 . Belyi functions may be described combinatorially by dessins d'enfants.
. Belyi functions may be described combinatorially by dessins d'enfants.Belyi functions and dessins d'enfants – but not Belyi's theorem – date at least to the work of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
; he used them in his to study an 11-fold cover of the complex projective line with monodromy group PSL(2,11).
Applications
Belyi's theorem is an existence theoremExistence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
for Belyi functions, and has subsequently been much used in the inverse Galois problem
Inverse Galois problem
In Galois theory, the inverse Galois problem concerns whether or not every finite group appears as the Galois group of some Galois extension of the rational numbers Q. This problem, first posed in the 19th century, is unsolved....
.

