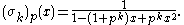Bell series
Encyclopedia
In mathematics
, the Bell series is a formal power series
used to study properties of arithmetical functions. Bell series were introduced and developed by Eric Temple Bell
.
Given an arithmetic function
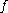and a prime
, define the formal power series 
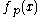, called the Bell series of 
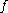modulo 
as:
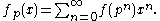
Two multiplicative functions can be shown to be identical if all of their Bell series are equal; this is sometimes called the uniqueness theorem. Given multiplicative function
s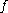
and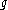 
, one has 
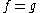if and only if
:
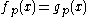for all primes 
.
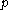Two series may be multiplied (sometimes called the multiplication theorem): For any two arithmetic function
s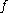
and 
, let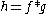 
be their Dirichlet convolution
. Then for every prime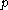
, one has:
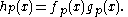
In particular, this makes it trivial to find the Bell series of a Dirichlet inverse
.
If
is completely multiplicative, then: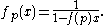
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bell series is a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
used to study properties of arithmetical functions. Bell series were introduced and developed by Eric Temple Bell
Eric Temple Bell
Eric Temple Bell , was a mathematician and science fiction author born in Scotland who lived in the U.S. for most of his life...
.
Given an arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
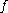and a primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
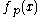, define the formal power series , called the Bell series of 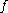modulo as: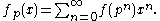Two multiplicative functions can be shown to be identical if all of their Bell series are equal; this is sometimes called the uniqueness theorem. Given multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
s
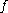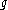and , one has 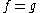if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
:
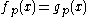for all primes 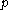.Two series may be multiplied (sometimes called the multiplication theorem): For any two arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
s
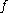and , let 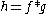be their Dirichlet convolutionDirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
. Then for every prime
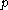, one has: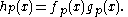In particular, this makes it trivial to find the Bell series of a Dirichlet inverse
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
.
If
is completely multiplicative, then: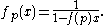Examples
The following is a table of the Bell series of well-known arithmetic functions.- The Moebius function
has 
- Euler's Totient
has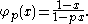 
- The multiplicative identity of the Dirichlet convolutionDirichlet convolutionIn mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
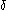has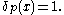 
- The Liouville function
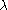has 
- The power function Idk has
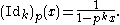Here, Idk is the completely multiplicative function 
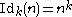. - The divisor functionDivisor functionIn mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
has 