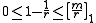Beatty sequence
Encyclopedia
In mathematics, a Beatty sequence (or homogeneous Beatty sequence) is the sequence of integers found by taking the floor of the positive multiples
of a positive irrational number
. Beatty sequences are named after Samuel Beatty
, who wrote about them in 1926.
Rayleigh's theorem, named after Lord Rayleigh, states that the complement
of a Beatty sequence, consisting of the positive integers that are not in the sequence, is itself a Beatty sequence generated by a different irrational number.
Beatty sequences can also be used to generate Sturmian word
s.
 generates the Beatty sequence
generates the Beatty sequence

If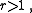 then
then 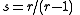 is also a positive irrational number. They naturally satisfy
is also a positive irrational number. They naturally satisfy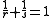
and the sequences and
and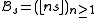
form a pair of complementary Beatty sequences.
A more general non-homogeneous Beatty sequence takes the form
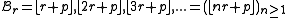
where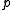 is a real number. For
is a real number. For 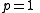 , the complementary non-homogeneous Beatty sequences can be found by making
, the complementary non-homogeneous Beatty sequences can be found by making 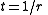 so that
so that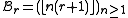 and
and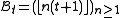
form a pair of complementary Beatty sequences. For other values of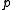 the procedure for finding complementary sequences is not as straightforward.
the procedure for finding complementary sequences is not as straightforward.
, we have s = r + 1. In this case, the sequence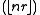 , known as the lower Wythoff sequence, is
, known as the lower Wythoff sequence, is
and the complementary sequence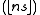 , the upper Wythoff sequence, is
, the upper Wythoff sequence, is
These sequences define the optimal strategy for Wythoff's game
.
As another example, for r = √2
, we have s = 2 + √2. In this case, the sequences are
Notice that any number in the first sequence is lacking in the second, and vice versa.
by Samuel Beatty
in 1926. It is probably one of the most often cited problems ever posed in the Monthly. However, even earlier, in 1894 such sequences were briefly mentioned by John W. Strutt (3rd Baron Rayleigh)
in the second edition of his book The Theory of Sound.
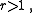 there exists
there exists 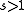 so that the Beatty sequences
so that the Beatty sequences 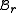 and
and 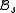 partition the set of positive integers: each positive integer belongs to exactly one of the two sequences.
partition the set of positive integers: each positive integer belongs to exactly one of the two sequences.
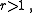 let
let  . We must show that every positive integer lies in one and only one of the two sequences
. We must show that every positive integer lies in one and only one of the two sequences 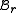 and
and 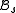 . We shall do so by considering the ordinal positions occupied by all the fractions j/r and k/s when they are jointly listed in nondecreasing order for positive integers j and k.
. We shall do so by considering the ordinal positions occupied by all the fractions j/r and k/s when they are jointly listed in nondecreasing order for positive integers j and k.
To see that no two of the numbers can occupy the same position (as a single number), suppose to the contrary that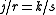 for some j and k. Then r/s = j/k, a rational number, but also,
for some j and k. Then r/s = j/k, a rational number, but also,  not a rational number. Therefore no two of the numbers occupy the same position.
not a rational number. Therefore no two of the numbers occupy the same position.
For any j/r, there are j numbers i/r ≤ j/r and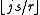 numbers
numbers 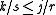 , so that the position of
, so that the position of 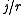 in the list is
in the list is  . The equation
. The equation 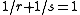 implies
implies
Likewise, the position of k/s in the list is .
.
Conclusion: every positive integer (that is, every position in the list) is of the form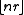 or of the form
or of the form 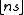 , but not both. The converse statement is also true: if p and q are two real numbers such that every positive integer occurs precisely once in the above list, then p and q are irrational and the sum of their reciprocals is 1.
, but not both. The converse statement is also true: if p and q are two real numbers such that every positive integer occurs precisely once in the above list, then p and q are irrational and the sum of their reciprocals is 1.
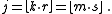
This is equivalent to the inequalities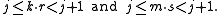
For non-zero j, the irrationality of r and s is incompatible with equality, so
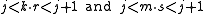
which lead to
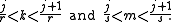
Adding these together and using the hypothesis, we get
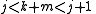
which is impossible (one cannot have an integer between two adjacent integers). Thus the supposition must be false.
Anti-collisions: Suppose that, contrary to the theorem, there are integers j > 0 and k and m such that
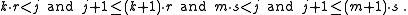
Since j + 1 is non-zero and r and s are irrational, we can exclude equality, so
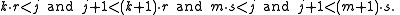
Then we get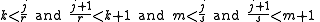
Adding corresponding inequalities, we get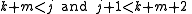

which is also impossible. Thus the supposition is false.
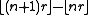
of the Beatty sequence associated to the irrational number is a characteristic Sturmian word
is a characteristic Sturmian word
over the alphabet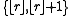 .
.
Multiple (mathematics)
In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of a positive irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Beatty sequences are named after Samuel Beatty
Samuel Beatty (mathematician)
Samuel Beatty was dean of the Faculty of Mathematics at the University of Toronto Mississauga, taking the position in 1934.-Early life:Beatty was born in 1881...
, who wrote about them in 1926.
Rayleigh's theorem, named after Lord Rayleigh, states that the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a Beatty sequence, consisting of the positive integers that are not in the sequence, is itself a Beatty sequence generated by a different irrational number.
Beatty sequences can also be used to generate Sturmian word
Sturmian word
In mathematics, a Sturmian word, named after Jacques Charles François Sturm, is a certain kind of infinite word.- Definition :A word is a infinite sequence of symbols drawn from a finite alphabet. Call any finite contiguous subsequence of a word a factor...
s.
Definition
A positive irrational number generates the Beatty sequence
generates the Beatty sequence
If
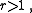 then
then 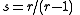 is also a positive irrational number. They naturally satisfy
is also a positive irrational number. They naturally satisfy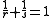
and the sequences
 and
and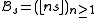
form a pair of complementary Beatty sequences.
A more general non-homogeneous Beatty sequence takes the form
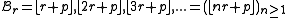
where
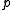 is a real number. For
is a real number. For 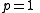 , the complementary non-homogeneous Beatty sequences can be found by making
, the complementary non-homogeneous Beatty sequences can be found by making 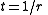 so that
so that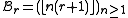 and
and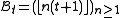
form a pair of complementary Beatty sequences. For other values of
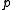 the procedure for finding complementary sequences is not as straightforward.
the procedure for finding complementary sequences is not as straightforward.Examples
For r = the golden meanGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, we have s = r + 1. In this case, the sequence
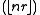 , known as the lower Wythoff sequence, is
, known as the lower Wythoff sequence, is
- 1, 3, 4, 6, 8, 9, 1111 (number)11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
, 1212 (number)12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 1414 (number)14 is the natural number following 13 and preceding 15.In speech, the numbers 14 and 40 are often confused. When carefully enunciated, they differ in which syllable is stressed: 14 vs 40...
, 1616 (number)16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and ....
, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 1919 (number)19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 2121 (number)21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 2222 (number)22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11....
, 2424 (number)24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
, 2525 (number)25 is the natural number following 24 and preceding 26.-In mathematics:It is a square number, being 5² = 5 × 5. It is the smallest square that is also a sum of two squares: 25 = 3² + 4²...
, 2727 (number)27 is the natural number following 26 and preceding 28.- In mathematics :Twenty-seven is a perfect cube, being 33 = 3 × 3 × 3. 27 is also 23 . There are exactly 27 straight lines on a smooth cubic surface, which give a basis of the fundamental representation of the E6 Lie algebra...
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, ... .
and the complementary sequence
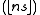 , the upper Wythoff sequence, is
, the upper Wythoff sequence, is
- 2, 5, 7, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 1515 (number)15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 1818 (number)18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress...
, 2020 (number)20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems....
, 2323 (number)23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime...
, 2626 (number)26 is the natural number following 25 and preceding 27.- In mathematics :26 is the only positive integer that is one greater than a square and one less than a cube .A rhombicuboctahedron has twenty-six sides....
, 2828 (number)28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14....
, 3131 (number)31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,...
, 3434 (number)34 is the natural number following 33 and preceding 35.-In mathematics:34 is the ninth distinct semiprime and has four divisors including unity and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers...
, 3636 (number)36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number...
, 3939 (number)39 is the natural number following 38 and preceding 40.- In mathematics :Thirty-nine is the sum of five consecutive primes and the sum of the first three powers of 3...
, 4141 (number)41 is the natural number following 40 and preceding 42.-In mathematics:Forty-one is the 13th smallest prime number. The next is forty-three, with which it comprises a twin prime...
, 4444 (number)44 is the natural number following 43 and preceding 45.- In mathematics :Forty-four is a tribonacci number, a happy number, an octahedral number and a palindromic number....
, 4747 (number)47 is the natural number following 46 and preceding 48.-In mathematics:Forty-seven is the fifteenth prime number, a safe prime, the thirteenth supersingular prime, and the sixth Lucas prime. Forty-seven is a highly cototient number...
, ... .
These sequences define the optimal strategy for Wythoff's game
Wythoff's game
Wythoff's game is a two-player mathematical game of strategy, played with two piles of counters. Players take turns removing counters from one or both piles; in the latter case, the numbers of counters removed from each pile must be equal...
.
As another example, for r = √2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, we have s = 2 + √2. In this case, the sequences are
- 1, 2, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 18, 19, 21, 22, 24, ... and
- 3, 6, 10, 13, 17, 20, 23, 27, 30, 34, 37, 40, 44, 47, 51, 54, 58, ... .
Notice that any number in the first sequence is lacking in the second, and vice versa.
History
Beatty sequences got their name from the problem posed in the American Mathematical MonthlyAmerican Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
by Samuel Beatty
Samuel Beatty (mathematician)
Samuel Beatty was dean of the Faculty of Mathematics at the University of Toronto Mississauga, taking the position in 1934.-Early life:Beatty was born in 1881...
in 1926. It is probably one of the most often cited problems ever posed in the Monthly. However, even earlier, in 1894 such sequences were briefly mentioned by John W. Strutt (3rd Baron Rayleigh)
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
in the second edition of his book The Theory of Sound.
Rayleigh theorem
The Rayleigh theorem (also known as Beatty's theorem) states that given an irrational number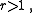 there exists
there exists 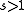 so that the Beatty sequences
so that the Beatty sequences 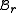 and
and 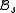 partition the set of positive integers: each positive integer belongs to exactly one of the two sequences.
partition the set of positive integers: each positive integer belongs to exactly one of the two sequences.First proof
Given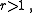 let
let  . We must show that every positive integer lies in one and only one of the two sequences
. We must show that every positive integer lies in one and only one of the two sequences 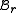 and
and 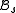 . We shall do so by considering the ordinal positions occupied by all the fractions j/r and k/s when they are jointly listed in nondecreasing order for positive integers j and k.
. We shall do so by considering the ordinal positions occupied by all the fractions j/r and k/s when they are jointly listed in nondecreasing order for positive integers j and k.To see that no two of the numbers can occupy the same position (as a single number), suppose to the contrary that
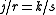 for some j and k. Then r/s = j/k, a rational number, but also,
for some j and k. Then r/s = j/k, a rational number, but also,  not a rational number. Therefore no two of the numbers occupy the same position.
not a rational number. Therefore no two of the numbers occupy the same position.For any j/r, there are j numbers i/r ≤ j/r and
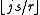 numbers
numbers 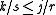 , so that the position of
, so that the position of 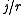 in the list is
in the list is  . The equation
. The equation 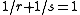 implies
impliesLikewise, the position of k/s in the list is
 .
.Conclusion: every positive integer (that is, every position in the list) is of the form
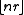 or of the form
or of the form 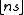 , but not both. The converse statement is also true: if p and q are two real numbers such that every positive integer occurs precisely once in the above list, then p and q are irrational and the sum of their reciprocals is 1.
, but not both. The converse statement is also true: if p and q are two real numbers such that every positive integer occurs precisely once in the above list, then p and q are irrational and the sum of their reciprocals is 1.Second proof
Collisions: Suppose that, contrary to the theorem, there are integers j > 0 and k and m such that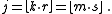
This is equivalent to the inequalities
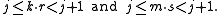
For non-zero j, the irrationality of r and s is incompatible with equality, so
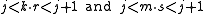
which lead to
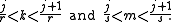
Adding these together and using the hypothesis, we get
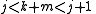
which is impossible (one cannot have an integer between two adjacent integers). Thus the supposition must be false.
Anti-collisions: Suppose that, contrary to the theorem, there are integers j > 0 and k and m such that
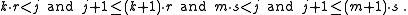
Since j + 1 is non-zero and r and s are irrational, we can exclude equality, so
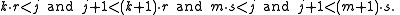
Then we get
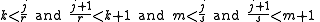
Adding corresponding inequalities, we get
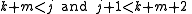

which is also impossible. Thus the supposition is false.
Properties
-
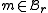 if and only
if and only
-
- where
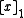 denotes
denotes  or the fractional part of
or the fractional part of  i.e.,
i.e.,  . Furthermore, if
. Furthermore, if 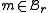
- Proof:
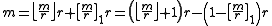
- If
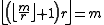 , then
, then 
- Or,
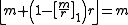 and thus,
and thus,  which is the given condition rearranged.
which is the given condition rearranged.
Relation with Sturmian sequences
The first difference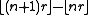
of the Beatty sequence associated to the irrational number
 is a characteristic Sturmian word
is a characteristic Sturmian wordSturmian word
In mathematics, a Sturmian word, named after Jacques Charles François Sturm, is a certain kind of infinite word.- Definition :A word is a infinite sequence of symbols drawn from a finite alphabet. Call any finite contiguous subsequence of a word a factor...
over the alphabet
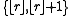 .
.Generalizations
The Lambek–Moser theorem generalizes the Rayleigh theorem and shows that more general pairs of sequences defined from an integer function and its inverse have the same property of partitioning the integers.External links
- Alexander Bogomolny, Beatty Sequences, Cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...