
Bauer-Fike theorem
Encyclopedia
In mathematics
, the Bauer–Fike theorem is a standard result in the perturbation theory
of the eigenvalue of a complex-valued diagonalizable matrix. In its substance, it states an absolute upper bound for the deviation of one perturbed matrix eigenvalue from a properly chosen eigenvalue of the exact matrix. Informally speaking, what it says is that the sensitivity of the eigenvalues is estimated by the condition number of the matrix of eigenvectors.
Theorem (Friedrich L. Bauer
Let 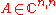 be a diagonalizable matrix, and
be a diagonalizable matrix, and 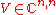 be the non singular eigenvector matrix such that
be the non singular eigenvector matrix such that 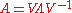 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that:
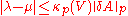
where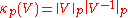 is the usual condition number
is the usual condition number
in p-norm.
 , we can choose
, we can choose  and the thesis is trivially verified (since
and the thesis is trivially verified (since 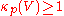 ).
).
So, be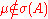 . Then
. Then 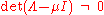 .
.  being an eigenvalue of
being an eigenvalue of  , we have
, we have 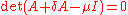 and so
and so
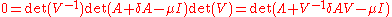
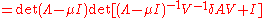
and, since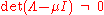 as stated above, we must have
as stated above, we must have
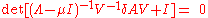
which reveals the value −1 to be an eigenvalue of the matrix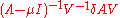 .
.
For each consistent matrix norm, we have , so, all p-norms being consistent, we can write:
, so, all p-norms being consistent, we can write:
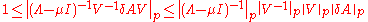
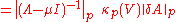
But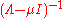 being a diagonal matrix, the p-norm is easily computed, and yields:
being a diagonal matrix, the p-norm is easily computed, and yields:
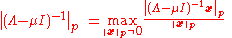
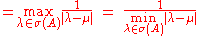
whence:
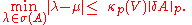
The theorem can also be reformulated to better suit numerical methods.
In fact, dealing with real eigensystem problems, one often has an exact matrix , but knows only an approximate eigenvalue-eigenvector couple, (
, but knows only an approximate eigenvalue-eigenvector couple, (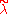 ,
, ), and needs to bound the error. The following version comes in help.
), and needs to bound the error. The following version comes in help.
Theorem (Friedrich L. Bauer
Let 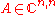 be a diagonalizable matrix, and be
be a diagonalizable matrix, and be 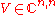 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 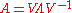 . Be moreover (
. Be moreover (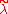 ,
, ) an approximate eigenvalue-eigenvector couple, and
) an approximate eigenvalue-eigenvector couple, and  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that:
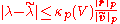
where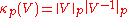 is the usual condition number
is the usual condition number
in p-norm.
m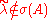 (otherwise, we can choose
(otherwise, we can choose  and theorem is proven, since
and theorem is proven, since 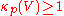 ).
).
Then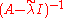 exists, so we can write:
exists, so we can write:
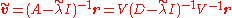
since is diagonalizable; taking the p-norm of both sides, we obtain:
is diagonalizable; taking the p-norm of both sides, we obtain:

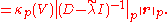
But, since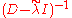 is a diagonal matrix, the p-norm is easily computed, and yields:
is a diagonal matrix, the p-norm is easily computed, and yields:
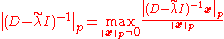
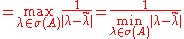
whence:
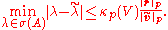
The Bauer–Fike theorem, in both versions, yields an absolute bound. The following corollary, which, besides all the hypothesis of Bauer–Fike theorem, requires also the non-singularity of A, turns out to be useful whenever a relative bound is needed.
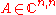 a non-singular, diagonalizable matrix, and be
a non-singular, diagonalizable matrix, and be 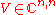 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 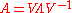 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that:
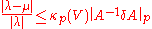
(Note: can be formally viewed as the "relative variation of A", just as
can be formally viewed as the "relative variation of A", just as 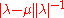 is the relative variation of λ.)
is the relative variation of λ.)
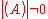 , we have, left-multiplying by
, we have, left-multiplying by 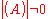 :
:
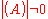
that is, putting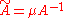 and
and  :
:
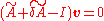
which means that is an eigenvalue of
is an eigenvalue of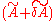 , with
, with  eigenvector. Now, the eigenvalues of
eigenvector. Now, the eigenvalues of 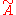 are
are 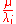 , while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix
, while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix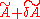 and to its eigenvalue
and to its eigenvalue , we obtain:
, we obtain:
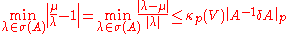
, V is a unitary matrix, and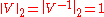 , so that
, so that 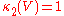 .
.
The Bauer–Fike theorem then becomes:
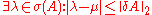
which obviously remains true if A is a Hermitian matrix. In this case, however, a much stronger result holds, known as the Weyl theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bauer–Fike theorem is a standard result in the perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of the eigenvalue of a complex-valued diagonalizable matrix. In its substance, it states an absolute upper bound for the deviation of one perturbed matrix eigenvalue from a properly chosen eigenvalue of the exact matrix. Informally speaking, what it says is that the sensitivity of the eigenvalues is estimated by the condition number of the matrix of eigenvectors.
Theorem (Friedrich L. BauerFriedrich L. BauerFriedrich Ludwig Bauer is a German computer scientist and professor emeritus at Technical University of Munich.-Life:...
, C.T.Fike – 1960)
Let 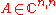 be a diagonalizable matrix, and
be a diagonalizable matrix, and 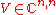 be the non singular eigenvector matrix such that
be the non singular eigenvector matrix such that 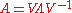 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that: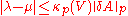
where
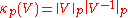 is the usual condition number
is the usual condition numberCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
in p-norm.
Proof
If , we can choose
, we can choose  and the thesis is trivially verified (since
and the thesis is trivially verified (since 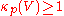 ).
).So, be
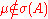 . Then
. Then 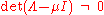 .
.  being an eigenvalue of
being an eigenvalue of  , we have
, we have 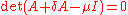 and so
and so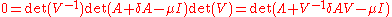
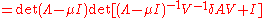
and, since
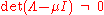 as stated above, we must have
as stated above, we must have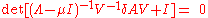
which reveals the value −1 to be an eigenvalue of the matrix
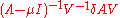 .
.For each consistent matrix norm, we have
 , so, all p-norms being consistent, we can write:
, so, all p-norms being consistent, we can write: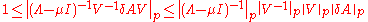
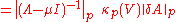
But
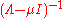 being a diagonal matrix, the p-norm is easily computed, and yields:
being a diagonal matrix, the p-norm is easily computed, and yields: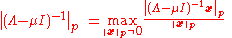
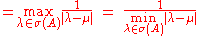
whence:
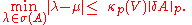
The theorem can also be reformulated to better suit numerical methods.
In fact, dealing with real eigensystem problems, one often has an exact matrix
 , but knows only an approximate eigenvalue-eigenvector couple, (
, but knows only an approximate eigenvalue-eigenvector couple, (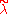 ,
, ), and needs to bound the error. The following version comes in help.
), and needs to bound the error. The following version comes in help.Theorem (Friedrich L. BauerFriedrich L. BauerFriedrich Ludwig Bauer is a German computer scientist and professor emeritus at Technical University of Munich.-Life:...
, C.T.Fike – 1960) (alternative statement)
Let 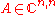 be a diagonalizable matrix, and be
be a diagonalizable matrix, and be 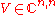 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 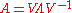 . Be moreover (
. Be moreover (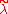 ,
, ) an approximate eigenvalue-eigenvector couple, and
) an approximate eigenvalue-eigenvector couple, and  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that: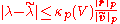
where
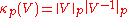 is the usual condition number
is the usual condition numberCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
in p-norm.
Proof
We solve this problem with Tarık's method:m
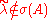 (otherwise, we can choose
(otherwise, we can choose  and theorem is proven, since
and theorem is proven, since 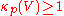 ).
).Then
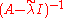 exists, so we can write:
exists, so we can write: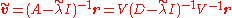
since
 is diagonalizable; taking the p-norm of both sides, we obtain:
is diagonalizable; taking the p-norm of both sides, we obtain:
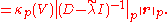
But, since
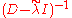 is a diagonal matrix, the p-norm is easily computed, and yields:
is a diagonal matrix, the p-norm is easily computed, and yields: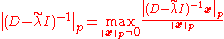
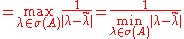
whence:
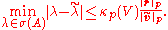
The Bauer–Fike theorem, in both versions, yields an absolute bound. The following corollary, which, besides all the hypothesis of Bauer–Fike theorem, requires also the non-singularity of A, turns out to be useful whenever a relative bound is needed.
Corollary
Be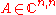 a non-singular, diagonalizable matrix, and be
a non-singular, diagonalizable matrix, and be 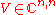 the non singular eigenvector matrix such as
the non singular eigenvector matrix such as 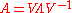 . Be moreover
. Be moreover  an eigenvalue of the matrix
an eigenvalue of the matrix  ; then an eigenvalue
; then an eigenvalue  exists such that:
exists such that: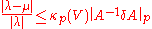
(Note:
 can be formally viewed as the "relative variation of A", just as
can be formally viewed as the "relative variation of A", just as 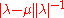 is the relative variation of λ.)
is the relative variation of λ.)Proof
Since μ is an eigenvalue of (A+δA) and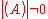 , we have, left-multiplying by
, we have, left-multiplying by 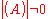 :
: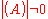
that is, putting
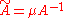 and
and  :
: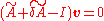
which means that
 is an eigenvalue of
is an eigenvalue of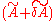 , with
, with  eigenvector. Now, the eigenvalues of
eigenvector. Now, the eigenvalues of 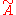 are
are 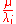 , while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix
, while its eigenvector matrix is the same as A. Applying the Bauer–Fike theorem to the matrix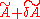 and to its eigenvalue
and to its eigenvalue , we obtain:
, we obtain: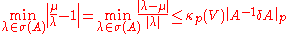
Remark
If A is normalNormal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, V is a unitary matrix, and
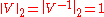 , so that
, so that 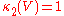 .
.The Bauer–Fike theorem then becomes:
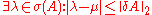
- |\lambda-\tilde{\lambda}|\leq\frac{\|\mathbf{r}\|_2}{\|\mathbf{\tilde{v}}\|_2} in the alternative formulation)
which obviously remains true if A is a Hermitian matrix. In this case, however, a much stronger result holds, known as the Weyl theorem.

