
Basset force
Encyclopedia
In a body submerged in a fluid
, unsteady forces due to acceleration
of that body with respect to the fluid, can be divided into two parts: the virtual mass effect and the Basset force.
The Basset force term describes the force due to the lagging boundary layer
development with changing relative velocity (acceleration) of bodies moving through a fluid.
The Basset term accounts for viscous
effects and addresses the temporal delay in boundary layer development as the relative velocity changes with time. It is also known as the "history" term.
The Basset force is difficult to implement and is commonly neglected for practical reasons; however, it can be substantially large when the body is accelerated at a high rate.
This force in an accelerating Stokes flow has been proposed by Joseph Valentin Boussinesq in 1885 and Alfred Barnard Basset in 1888. Consequently, it is also referred to as the Boussinesq–Basset force.
The equation of motion for the fluid—Stokes flow at low Reynolds number—is
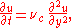
where u is the velocity of the fluid, at some time t, parallel to the plate, at a distance y from the plate, and νc is the kinematic viscosity of the fluid (c~continuous phase).
The solution to this equation is

where erf denotes the error function
.
Assuming that an acceleration of the plate can be broken up into a series of such step changes in the velocity, it can be shown that the cummulative effect on the shear stress on the plate is
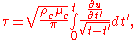
where ρc is the mass density of the fluid, and μc is the viscosity
of the fluid.
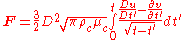 ,
,
where D is the particle diameter, is the material derivative, and u and v are the fluid and particle velocity vectors, respectively.
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
, unsteady forces due to acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of that body with respect to the fluid, can be divided into two parts: the virtual mass effect and the Basset force.
The Basset force term describes the force due to the lagging boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
development with changing relative velocity (acceleration) of bodies moving through a fluid.
The Basset term accounts for viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
effects and addresses the temporal delay in boundary layer development as the relative velocity changes with time. It is also known as the "history" term.
The Basset force is difficult to implement and is commonly neglected for practical reasons; however, it can be substantially large when the body is accelerated at a high rate.
This force in an accelerating Stokes flow has been proposed by Joseph Valentin Boussinesq in 1885 and Alfred Barnard Basset in 1888. Consequently, it is also referred to as the Boussinesq–Basset force.
Acceleration of a flat plate
Consider an infinitely large plate started impulsively with a step change in velocity from 0 to u0, in the direction of the plate–fluid interface plane.The equation of motion for the fluid—Stokes flow at low Reynolds number—is
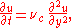
where u is the velocity of the fluid, at some time t, parallel to the plate, at a distance y from the plate, and νc is the kinematic viscosity of the fluid (c~continuous phase).
The solution to this equation is

where erf denotes the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
.
Assuming that an acceleration of the plate can be broken up into a series of such step changes in the velocity, it can be shown that the cummulative effect on the shear stress on the plate is
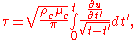
where ρc is the mass density of the fluid, and μc is the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of the fluid.
Acceleration of a spherical particle
Boussinesq (1885) and Basset (1888) found that the force F on an accelerating spherical particle in a viscous fluid is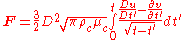 ,
,where D is the particle diameter, is the material derivative, and u and v are the fluid and particle velocity vectors, respectively.

