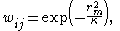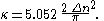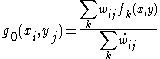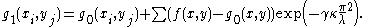Barnes interpolation
Encyclopedia
Barnes interpolation, named after Stanley L. Barnes, is the interpolation
of unstructured data points from a set of measurements of an unknown function in two dimensions into an analytic function
of two variables. An example of a situation where the Barnes scheme is important is in weather forecasting
where measurements are made wherever monitoring stations may be located, the positions of which are constrained by topography
. Such interpolation is essential in data visualisation, e.g. in the construction of contour plots or other representations of analytic surfaces.
The method constructs a grid of size determined by the distribution of the two dimensional data points. Using this grid, the function values are calculated at each grid point. To do this the method utilises a series of Gaussian functions, given a distance weighting in order to determine the relative importance of any given measurement on the determination of the function values. Correction passes are then made to optimise the function values, by accounting for the spectral response of the interpolated points.
where is a falloff parameter that controls the width of the Gaussian function. This parameter is controlled by the characteristic data spacing, for a fixed Gaussian cutoff radius wij = e−1 giving Δn such that:
is a falloff parameter that controls the width of the Gaussian function. This parameter is controlled by the characteristic data spacing, for a fixed Gaussian cutoff radius wij = e−1 giving Δn such that:
The initial interpolation for the function from the measured values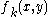 then becomes:
then becomes:
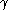 as well as the influence the final result. Guidelines for the selection of these parameters have been suggested, however the final values used are free to be chosen within these guidelines.
as well as the influence the final result. Guidelines for the selection of these parameters have been suggested, however the final values used are free to be chosen within these guidelines.
The data spacing used in the analysis, Δn may be chosen either by calculating the true experimental data inter-point spacing, or by the use of a complete spatial randomness
assumption, depending upon the degree of clustering
in the observed data. The smoothing parameter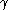 is constrained to be between 0.2 and 1.0. For reasons of interpolation integrity, Δx is argued to be constrained between 0.3 and 0.5.
is constrained to be between 0.2 and 1.0. For reasons of interpolation integrity, Δx is argued to be constrained between 0.3 and 0.5.
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
of unstructured data points from a set of measurements of an unknown function in two dimensions into an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
of two variables. An example of a situation where the Barnes scheme is important is in weather forecasting
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
where measurements are made wherever monitoring stations may be located, the positions of which are constrained by topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
. Such interpolation is essential in data visualisation, e.g. in the construction of contour plots or other representations of analytic surfaces.
Introduction
Barnes proposed an objective scheme for the interpolation of two dimensional data using a multi-pass scheme. This provided a method to interpolating sea-level pressures across the entire United States of America, producing a synoptic chart across the country using dispersed monitoring stations. Researchers have subsequently improved the Barnes method to reduce the number of parameters required for calculation of the interpolated result, increasing the objectivity of the method.The method constructs a grid of size determined by the distribution of the two dimensional data points. Using this grid, the function values are calculated at each grid point. To do this the method utilises a series of Gaussian functions, given a distance weighting in order to determine the relative importance of any given measurement on the determination of the function values. Correction passes are then made to optimise the function values, by accounting for the spectral response of the interpolated points.
First pass
For a given grid point i, j the interpolated function g(xi, yi) is first approximated by the inverse weighting of the data points. To do this as weighting values is assigned to each Gaussian for each grid point, such thatwhere
 is a falloff parameter that controls the width of the Gaussian function. This parameter is controlled by the characteristic data spacing, for a fixed Gaussian cutoff radius wij = e−1 giving Δn such that:
is a falloff parameter that controls the width of the Gaussian function. This parameter is controlled by the characteristic data spacing, for a fixed Gaussian cutoff radius wij = e−1 giving Δn such that:The initial interpolation for the function from the measured values
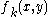 then becomes:
then becomes:Second pass
The correction for the next pass then utilises the difference between the observed field and the interpolated values at the measurement points to optimise the result:Parameter selection
Although described as an objective method, there are many parameters which control the interpolated field. The choice of Δn, grid spacing Δx and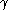 as well as the influence the final result. Guidelines for the selection of these parameters have been suggested, however the final values used are free to be chosen within these guidelines.
as well as the influence the final result. Guidelines for the selection of these parameters have been suggested, however the final values used are free to be chosen within these guidelines.The data spacing used in the analysis, Δn may be chosen either by calculating the true experimental data inter-point spacing, or by the use of a complete spatial randomness
Complete spatial randomness
Complete spatial randomness describes a point process whereby point events occur within a given study area in a completely random fashion. Such a process is often modeled using only one parameter, i.e. the density of points, \rho within the defined area...
assumption, depending upon the degree of clustering
Clustering
Clustering can refer to the following:In demographics:* Clustering , the gathering of various populations based on factors such as ethnicity, economics or religion.In graph theory:...
in the observed data. The smoothing parameter
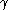 is constrained to be between 0.2 and 1.0. For reasons of interpolation integrity, Δx is argued to be constrained between 0.3 and 0.5.
is constrained to be between 0.2 and 1.0. For reasons of interpolation integrity, Δx is argued to be constrained between 0.3 and 0.5.