
Balian-Low theorem
Encyclopedia
In mathematics
, the Balian–Low theorem in Fourier analysis is named for Roger Balian
and Francis E. Low
.
The theorem states that no Gabor frame
has a window function (or Gabor atom) g which is well-localized in both time and frequency.
Suppose g is a square-integrable function
on the real line
, and consider the so-called Gabor system
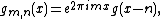
for integers m and n. The Balian–Low theorem states that if
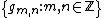
is an orthonormal basis
for the Hilbert space

then either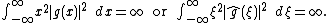
The Balian–Low theorem has been extended to exact Gabor frames
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Balian–Low theorem in Fourier analysis is named for Roger Balian
Roger Balian
Roger Balian is a French physicist who has worked on quantum thermodynamics and theory of measurement.Balian is a member of French Académie des sciences . His important work includes the Balian-Low theorem. He teaches statistical physics at the École Polytechnique.-References:...
and Francis E. Low
Francis E. Low
Francis Eugene Low was an American theoretical physicist. He was an Institute Professor at MIT, and served as provost there from 1980 to 1985.-Early career:...
.
The theorem states that no Gabor frame
Frame of a vector space
In linear algebra, a frame of a vector space V with an inner product can be seen as a generalization of the idea of a basis to sets which may be linearly dependent...
has a window function (or Gabor atom) g which is well-localized in both time and frequency.
Suppose g is a square-integrable function
Square-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, and consider the so-called Gabor system
Dennis Gabor
Dennis Gabor CBE, FRS was a Hungarian-British electrical engineer and inventor, most notable for inventing holography, for which he later received the 1971 Nobel Prize in Physics....
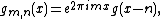
for integers m and n. The Balian–Low theorem states that if
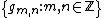
is an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

then either
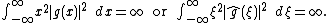
The Balian–Low theorem has been extended to exact Gabor frames
Frame of a vector space
In linear algebra, a frame of a vector space V with an inner product can be seen as a generalization of the idea of a basis to sets which may be linearly dependent...
.

