
Frame of a vector space
Encyclopedia
In linear algebra
, a frame of a vector space V with an inner product can be seen as a generalization of the idea of a basis
to sets which may be linearly dependent. The key issue related to the construction of a frame appears when we have a sequence of vectors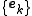 , with each
, with each 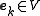 and we want to express an arbitrary element
and we want to express an arbitrary element 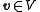 as a linear combination of the vectors
as a linear combination of the vectors 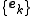 :
:
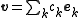
and want to determine the coefficients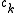 . If the set
. If the set  does not span
does not span 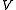 , then these coefficients cannot be determined for all such
, then these coefficients cannot be determined for all such  . If
. If  spans
spans  and also is linearly independent, this set forms a basis
and also is linearly independent, this set forms a basis
of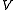 , and the coefficients
, and the coefficients 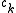 are uniquely determined by
are uniquely determined by  : they are the coordinates of
: they are the coordinates of  relative to this basis. If, however,
relative to this basis. If, however, 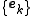 spans
spans 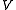 but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if
but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if 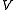 is of infinite dimension.
is of infinite dimension.
Given that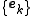 spans
spans 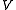 and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:
and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:
In 1952, Duffin and Schaeffer gave a solution to this problem, by describing a condition on the set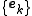 that makes it possible to compute the coefficients
that makes it possible to compute the coefficients 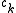 in a simple way. More precisely, a frame is a set
in a simple way. More precisely, a frame is a set 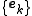 of elements of V which satisfy the so-called frame condition:
of elements of V which satisfy the so-called frame condition:
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a frame of a vector space V with an inner product can be seen as a generalization of the idea of a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
to sets which may be linearly dependent. The key issue related to the construction of a frame appears when we have a sequence of vectors
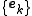 , with each
, with each 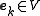 and we want to express an arbitrary element
and we want to express an arbitrary element 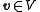 as a linear combination of the vectors
as a linear combination of the vectors 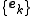 :
: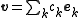
and want to determine the coefficients
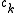 . If the set
. If the set  does not span
does not span 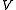 , then these coefficients cannot be determined for all such
, then these coefficients cannot be determined for all such  . If
. If  spans
spans  and also is linearly independent, this set forms a basis
and also is linearly independent, this set forms a basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of
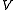 , and the coefficients
, and the coefficients 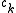 are uniquely determined by
are uniquely determined by  : they are the coordinates of
: they are the coordinates of  relative to this basis. If, however,
relative to this basis. If, however, 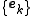 spans
spans 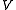 but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if
but is not linearly independent, the question of how to determine the coefficients becomes less apparent, in particular if 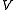 is of infinite dimension.
is of infinite dimension.Given that
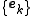 spans
spans 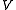 and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:
and is linearly dependent, it may appear obvious that we should remove vectors from the set until it becomes linearly independent and forms a basis. There are some problems with this strategy:- By removing vectors randomly from the set, it may lose its possibility to span
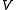 before it becomes linearly independent.
before it becomes linearly independent. - Even if it is possible to devise a specific way to remove vectors from the set until it becomes a basis, this approach may become infeasible in practice if the set is large or infinite.
- In some applications, it may be an advantage to use more vectors than necessary to represent
 . This means that we want to find the coefficients
. This means that we want to find the coefficients  without removing elements in
without removing elements in 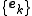 .
.
In 1952, Duffin and Schaeffer gave a solution to this problem, by describing a condition on the set
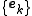 that makes it possible to compute the coefficients
that makes it possible to compute the coefficients 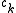 in a simple way. More precisely, a frame is a set
in a simple way. More precisely, a frame is a set 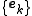 of elements of V which satisfy the so-called frame condition:
of elements of V which satisfy the so-called frame condition:- There exist two real numbers, A and B such that
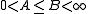 and
and
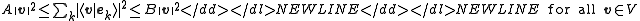 .
.
- This means that the constants A and B can be chosen independently of v: they only depend on the set
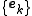 .
.
The numbers A and B are called lower and upper frame bounds.
It can be shown that the frame condition is both necessary and sufficient to form a frame a set of dual frame vectors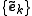 with the following property:
with the following property:
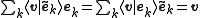
for any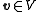 . This implies that a frame together with its dual frame has the same properties as a basis and its dual basis in terms of reconstructing a vector from scalar products.
. This implies that a frame together with its dual frame has the same properties as a basis and its dual basis in terms of reconstructing a vector from scalar products.
Relation to bases
If the set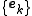 is a frame of V, it spans V. Otherwise there would exist at least one non-zero
is a frame of V, it spans V. Otherwise there would exist at least one non-zero 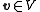 which would be orthogonal to all
which would be orthogonal to all 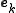 . If we insert
. If we insert  into the frame condition, we obtain
into the frame condition, we obtain
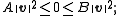
therefore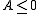 , which is a violation of the initial assumptions on the lower frame bound.
, which is a violation of the initial assumptions on the lower frame bound.
If a set of vectors spans V, this is not a sufficient condition for calling the set a frame. As an example, consider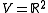 and the infinite set
and the infinite set  given by
given by
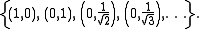
This set spans V but since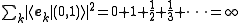 we cannot choose
we cannot choose 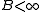 . Consequently, the set
. Consequently, the set  is not a frame.
is not a frame.
Tight frames
A frame is tight if the frame bounds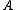 and
and 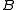 are equal. This means that the frame obeys a generalized Parseval's identityParseval's identityIn mathematical analysis, Parseval's identity is a fundamental result on the summability of the Fourier series of a function. Geometrically, it is thePythagorean theorem for inner-product spaces....
are equal. This means that the frame obeys a generalized Parseval's identityParseval's identityIn mathematical analysis, Parseval's identity is a fundamental result on the summability of the Fourier series of a function. Geometrically, it is thePythagorean theorem for inner-product spaces....
. If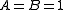 , then a frame is either called normalized or Parseval. However, some of the literature refers to a frame for which
, then a frame is either called normalized or Parseval. However, some of the literature refers to a frame for which  where
where  is a constant independent of
is a constant independent of 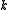 (see uniform below) as a normalized frame.
(see uniform below) as a normalized frame.
Uniform frames
A frame is uniform if each element has the same norm: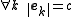 where
where  is a constant independent of
is a constant independent of  .
.
A uniform normalized tight frame with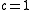 is an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
is an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
.
The dual frame
The frame condition is both sufficient and necessary for allowing the construction of a dual or conjugate frame,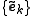 , relative the original frame,
, relative the original frame, 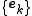 . The duality of this frame implies that
. The duality of this frame implies that
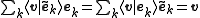
is satisfied for all . In order to construct the dual frame, we first need the linear mapping:
. In order to construct the dual frame, we first need the linear mapping: 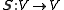 defined as
defined as
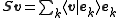
From this definition of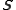 and linearity in the first argument of the inner product, it now follows that
and linearity in the first argument of the inner product, it now follows that
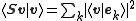
which can be inserted into the frame condition to get
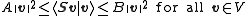
The properties of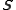 can be summarised as follows:
can be summarised as follows:
-
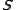 is self-adjointSelf-adjointIn mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
is self-adjointSelf-adjointIn mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
, positive definite, and has positive upper and lower bounds. This leads to - the inverse
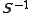 of
of 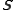 exists and it, too, is self-adjoint, positive definite, and has positive upper and lower bounds.
exists and it, too, is self-adjoint, positive definite, and has positive upper and lower bounds.
The dual frame is defined by mapping each element of the frame with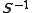 :
:
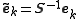
To see that this make sense, let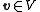 be arbitrary and set
be arbitrary and set

It is then the case that
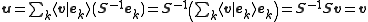
which proves that

Alternatively, we can set
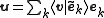
By inserting the above definition of and applying known properties of
and applying known properties of 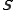 and its inverse, we get
and its inverse, we get

which shows that
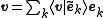
This derivation of the dual frame is a summary of section 3 in the article by Duffin and Schaeffer. They use the term conjugate frame for what here is called dual frame.
History
Frames were introduced by Duffin and Schaeffer in their study on nonharmonic Fourier series. They remained obscure until MallatStéphane MallatStéphane G. Mallat made some fundamental contributions to the development of wavelet theory in the late 1980s and early 1990s...
, DaubechiesIngrid DaubechiesIngrid Daubechies is a Belgian physicist and mathematician. She was between 2004 and 2011 the William R. Kenan Jr. Professor in the mathematics and applied mathematics departments at Princeton University. In January 2011 she moved to Duke University as a Professor in mathematics. She is the first...
, and others used them to analyze wavelets in the 1980s. Some practical uses of frames today include robust codingError detection and correctionIn information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
and design and analysis of filter bankFilter bankIn signal processing, a filter bank is an array of band-pass filters that separates the input signal into multiple components, each one carrying a single frequency subband of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components...
s.- This means that the constants A and B can be chosen independently of v: they only depend on the set

