
Balance puzzle
Encyclopedia
A number of logic puzzle
s exist that are based on the balancing of similar-looking items, often coins, to determine which one is of a different value within a limited number of uses of the balance scales. These differ from puzzles where items are assigned weights, in that only the relative mass of these items is relevant.
 A well-known example has nine (or fewer) items, say coins (or balls), that are identical in weight save for one, which in this example we will say is lighter than the others—a counterfeit (an oddball). The difference is only perceptible by using a pair of scales balance
A well-known example has nine (or fewer) items, say coins (or balls), that are identical in weight save for one, which in this example we will say is lighter than the others—a counterfeit (an oddball). The difference is only perceptible by using a pair of scales balance
, but only the coins themselves can be weighed.
Is it possible to isolate the counterfeit coin with only two weighings?
Now, assume we have three coins wrapped in a bigger coin-shaped box. In one move, we can find which of the three boxes is lighter (this box would contain the lighter coin) and, in the second weighing, as was shown above, we can find which of the three coins within the box is lighter. So in two weighings we can find a single light coin from a set of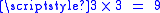 .
.
Note that we could reason along the same line, further, to see that in three weighings one can find the odd-lighter coin among 27 coins and in 4 weighings, from 81 coins.
With some outside the box
thinking, such as assuming that there are authentic (genuine) coins at hand, a solution may be found quicker. In fact if there is one authentic coin for reference then the suspect coins can be thirteen. Number the coins from 1 to 13 and the authentic coin number 0 and perform these weighings in any order:
If the scales are only off balance once, then it must be one of the coins 1, 2, 3 which only appear in one weighing.
If there is never balance then it must be one of the coins 10–13 that appear in all weighings. Picking out the one counterfeit coin corresponding to each of the 27 outcomes is always possible (13 coins one either too heavy or too light is 26 possibilities) except when all weighings are balanced, in which case there is no counterfeit coin (or its weight is correct). If coins 0 and 13 are deleted from these weighings they give one generic solution to the 12-coin problem.
In yet another variation, one only needs to find the counterfeit coin without necessarily being able to tell its weight relative to the others. In this case, the number of coins can be 13. The first two weighings are identical to the steps in the 12-coin problem described above, but with one extra leftover coin. The only other difference is in case 2c, where two coins are left instead of one. By weighing one of those coins against one of the 11 coins that are known to be good from the previous weighings, one can tell which is the counterfeit coin but, if it turns out to be the last coin, it will never have participated in any weighing so it is still unknown whether it is lighter of heavier.
Combining these variations, if extra coins are available and the weight of the counterfeit coin needs not to be determined, the maximum number of suspect coins is 14. In the first weighing, 5 suspect coins are weighed against 4 other suspect coins and one good coin, while leaving 5 aside. If the side with 5 suspect coins is heavier, either one of the 5 coins is heavier or one of the 4 coins is lighter. Place 2 of the possibly light coins and one of the possibly heavy coins on each side of the balance. If it balances out, the counterfeit coin is among the three coins that were used in the first but not in the second weighing, and is heavier, so it can be found by weighing one against one other. All other possibilities are analogous to the solutions of the problems above.
's novel
With a Tangled Skein
, must solve the twelve-coin variation of this puzzle to find her son in Hell
: Satan
has disguised the son to look identical to eleven other demons, and he is heavier or lighter depending on whether he is cursed to lie or able to speak truthfully. The solution in the book follows the given example 1.c.
Logic puzzle
A logic puzzle is a puzzle deriving from the mathematics field of deduction.-History:The logic puzzle was first produced by Charles Lutwidge Dodgson, who is better known under his pen name Lewis Carroll, the author of Alice's Adventures in Wonderland...
s exist that are based on the balancing of similar-looking items, often coins, to determine which one is of a different value within a limited number of uses of the balance scales. These differ from puzzles where items are assigned weights, in that only the relative mass of these items is relevant.
Premise

Weighing scale
A weighing scale is a measuring instrument for determining the weight or mass of an object. A spring scale measures weight by the distance a spring deflects under its load...
, but only the coins themselves can be weighed.
Is it possible to isolate the counterfeit coin with only two weighings?
Solution
To find a solution to the problem we first consider the maximum number of items from which one can find the lighter one in just one weighing. The maximum number possible is three. To find the lighter one we can compare any two coins, leaving the third out. If the two coins tested weigh the same, then the lighter coin must be one of those not on the balance - otherwise it is the one indicated as lighter by the balance.Now, assume we have three coins wrapped in a bigger coin-shaped box. In one move, we can find which of the three boxes is lighter (this box would contain the lighter coin) and, in the second weighing, as was shown above, we can find which of the three coins within the box is lighter. So in two weighings we can find a single light coin from a set of
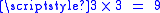 .
.Note that we could reason along the same line, further, to see that in three weighings one can find the odd-lighter coin among 27 coins and in 4 weighings, from 81 coins.
The twelve-coin problem
A more complex version exists where there are twelve coins, eleven of which are identical and one of which is different, but it is not known whether it is heavier or lighter than the others. This time the balance may be used three times to isolate the unique coin and determine its weight relative to the others.Solution
The procedure is less straightforward for this problem, and the second and third weighings depend on what has happened previously, although that need not be the case (see below).- Four coins are put on each side. There are two possibilities:
- 1. One side is heavier than the other. If this is the case, remove three coins from the heavier side, move three coins from the lighter side to the heavier side, and place three coins that were not weighed the first time on the lighter side. (Remember which coins are which.) There are three possibilities:
-
- 1.a) The same side that was heavier the first time is still heavier. This means that either the coin that stayed there is heavier or that the coin that stayed on the lighter side is lighter. Balancing one of these against one of the other ten coins will reveal which of these is true, thus solving the puzzle.
-
- 1.b) The side that was heavier the first time is lighter the second time. This means that one of the three coins that went from the lighter side to the heavier side is the light coin. For the third attempt, weigh two of these coins against each other: if one is lighter, it is the unique coin; if they balance, the third coin is the light one.
-
- 1.c) Both sides are even. This means the one of the three coins that was removed from the heavier side is the heavy coin. For the third attempt, weigh two of these coins against each other: if one is heavier, it is the unique coin; if they balance, the third coin is the heavy one.
- 2. Both sides are even. If this is the case, all eight coins are identical and can be set aside. Take the four remaining coins and place three on one side of the balance. Place 3 of the 8 identical coins on the other side. There are three possibilities:
-
- 2.a) The three remaining coins are lighter. In this case you now know that one of those three coins is the odd one out and that it is lighter. Take two of those three coins and weigh them against each other. If the balance tips then the lighter coin is the odd one out. If the two coins balance then the third coin not on the balance is the odd one out and it is lighter.
-
- 2.b) The three remaining coins are heavier. In this case you now know that one of those three coins is the odd one out and that it is heavier. Take two of those three coins and weigh them against each other. If the balance tips then the heavier coin is the odd one out. If the two coins balance then the third coin not on the balance is the odd one out and it is heavier.
-
- 2.c) The three remaining coins balance. In this case you know that the unweighed coin is the odd one out. Weigh the remaining coin against one of the other 11 coins and this will tell you whether it is heavier or lighter.
With some outside the box
Outside The Box
Outside The Box is Vicki Genfan's first available release and features both instrumental and vocal songs. It gained wide recognition and was highly acclaimed by critics...
thinking, such as assuming that there are authentic (genuine) coins at hand, a solution may be found quicker. In fact if there is one authentic coin for reference then the suspect coins can be thirteen. Number the coins from 1 to 13 and the authentic coin number 0 and perform these weighings in any order:
- 0, 1, 4, 5, 6 against 7, 10, 11, 12, 13
- 0, 2, 4, 10, 11 against 5, 8, 9, 12, 13
- 0, 3, 8, 10, 12 against 6, 7, 9, 11, 13
If the scales are only off balance once, then it must be one of the coins 1, 2, 3 which only appear in one weighing.
If there is never balance then it must be one of the coins 10–13 that appear in all weighings. Picking out the one counterfeit coin corresponding to each of the 27 outcomes is always possible (13 coins one either too heavy or too light is 26 possibilities) except when all weighings are balanced, in which case there is no counterfeit coin (or its weight is correct). If coins 0 and 13 are deleted from these weighings they give one generic solution to the 12-coin problem.
In yet another variation, one only needs to find the counterfeit coin without necessarily being able to tell its weight relative to the others. In this case, the number of coins can be 13. The first two weighings are identical to the steps in the 12-coin problem described above, but with one extra leftover coin. The only other difference is in case 2c, where two coins are left instead of one. By weighing one of those coins against one of the 11 coins that are known to be good from the previous weighings, one can tell which is the counterfeit coin but, if it turns out to be the last coin, it will never have participated in any weighing so it is still unknown whether it is lighter of heavier.
Combining these variations, if extra coins are available and the weight of the counterfeit coin needs not to be determined, the maximum number of suspect coins is 14. In the first weighing, 5 suspect coins are weighed against 4 other suspect coins and one good coin, while leaving 5 aside. If the side with 5 suspect coins is heavier, either one of the 5 coins is heavier or one of the 4 coins is lighter. Place 2 of the possibly light coins and one of the possibly heavy coins on each side of the balance. If it balances out, the counterfeit coin is among the three coins that were used in the first but not in the second weighing, and is heavier, so it can be found by weighing one against one other. All other possibilities are analogous to the solutions of the problems above.
In literature
Niobe, the protagonist of Piers AnthonyPiers Anthony
Piers Anthony Dillingham Jacob is an English American writer in the science fiction and fantasy genres, publishing under the name Piers Anthony. He is most famous for his long-running novel series set in the fictional realm of Xanth.Many of his books have appeared on the New York Times Best...
's novel
Novel
A novel is a book of long narrative in literary prose. The genre has historical roots both in the fields of the medieval and early modern romance and in the tradition of the novella. The latter supplied the present generic term in the late 18th century....
With a Tangled Skein
With a Tangled Skein
With a Tangled Skein is a fantasy novel by Piers Anthony. It is the third of eight books in the Incarnations of Immortality series.- Plot introduction :...
, must solve the twelve-coin variation of this puzzle to find her son in Hell
Hell
In many religious traditions, a hell is a place of suffering and punishment in the afterlife. Religions with a linear divine history often depict hells as endless. Religions with a cyclic history often depict a hell as an intermediary period between incarnations...
: Satan
Satan
Satan , "the opposer", is the title of various entities, both human and divine, who challenge the faith of humans in the Hebrew Bible...
has disguised the son to look identical to eleven other demons, and he is heavier or lighter depending on whether he is cursed to lie or able to speak truthfully. The solution in the book follows the given example 1.c.

