In physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, the Bak–Tang–Wiesenfeld sandpile model is the first discovered example of a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

 displaying self-organized criticality

Self-organized criticality

In physics, self-organized criticality is a property of dynamical systems which have a critical point as an attractor. Their macroscopic behaviour thus displays the spatial and/or temporal scale-invariance characteristic of the critical point of a phase transition, but without the need to tune...

 and is named after Per Bak

Per Bak

Per Bak was a Danish theoretical physicist who coauthored the 1987 academic paper that coined the term "self-organized criticality."- Life and work :...

, Chao Tang

Chao Tang

Chao Tang is a Chinese physicist and professor at the University of California at San Francisco.In 1987, as a post-doctoral research scientist in the Solid State Theory Group of Brookhaven National Laboratory, he and another fellow post-doctoral scientist, Kurt Wiesenfeld, along with their mentor,...

 and Kurt Wiesenfeld

Kurt Wiesenfeld

Kurt Wiesenfeld is an American physicist working primarily on non-linear dynamics. His works primarily concern stochastic resonance, spontaneous synchronization of coupled oscillators, and non-linear laser dynamics...

.

The model is a cellular automaton

Cellular automaton

A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...

. At each site on the lattice there is a value that corresponds to the slope of the pile. This slope builds up as grains of sand are randomly placed onto the pile, until the slope exceeds a specific threshold value at which time that site collapses transferring sand into the adjacent sites, increasing their slope. Thus random placement of sand at a particular site may have no effect, or it may cause a cascading reaction that will affect every site on the lattice. These "avalanches" are an example of the Eden growth model

Eden growth model

The Eden growth model describes the growth of specific types of clusters such as bacterial colonies and deposition of materials. These clusters grow by random accumulation of material on their boundary. These are also an example of a surface fractal....

.

The iteration rules for the 2D model are as follows:

Starting with a flat surface 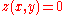for all x and y:

Add a grain of sand:
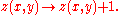
And avalanche if :

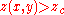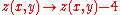
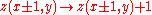
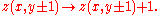
This system is interesting in that it is attracted to its critical state, at which point the correlation length of the system and the correlation time of the system go to infinity, without any fine tuning of a system parameter. This contrasts with earlier examples of critical phenomena, such as the phase transition

Phase transition

A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....

s between solid and liquid, or liquid and gas, where the critical point can only be reached by precise tuning (usually of temperature). Hence, in the sandpile model we can say that the criticality is self-organized

Self-organization

Self-organization is the process where a structure or pattern appears in a system without a central authority or external element imposing it through planning...

.

Once the sandpile model reaches its critical state there is no correlation between the system's response to a perturbation and the details of a perturbation. Generally this means that dropping another grain of sand onto the pile may cause nothing to happen, or it may cause the entire pile to collapse in a massive slide. The model also displays 1/f noise, a feature common to many complex systems in nature.

This model only displays critical behaviour in 2 or more dimensions. The sandpile model can be expressed in 1D; however, instead of evolving to its critical state, the 1D sandpile model instead reaches a minimally stable state where every lattice site goes toward the critical slope.

The iteration rules for the 1D model are:

Adding a grain of sand at :
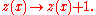
And an avalanche at if :

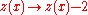
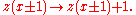
Cultural References

The Bak-Tang-Wiesenfeld sandpile was mentioned on the Numb3rs

NUMB3RS

Numb3rs is an American television drama which premiered on CBS on January 23, 2005, and concluded on March 12, 2010. The series was created by Nicolas Falacci and Cheryl Heuton, and follows FBI Special Agent Don Eppes and his mathematical genius brother, Charlie Eppes , who helps Don solve crimes...

episode "Rampage," as mathematician Charlie Eppes explains to his colleagues a solution to a criminal investigation.