
BCMP network
Encyclopedia
In queueing theory
, a discipline within the mathematical theory of probability
, a BCMP network is a class of queueing network
for which a product form equilibrium distribution
exists. It is named after the authors of the paper where the network was first described: Baskett, Chandy
, Muntz and Palacios. The theorem is a significant extension to a Jackson network allowing virtually arbitrary customer routing and service time distributions, subject to particular service disciplines.
The paper is well known, and the theorem was described in 1990 as "one of the seminal achievements in queueing theory in the last 20 years" by J. Michael Harrison
and Ruth Williams.
In the final three cases, service time distributions must have rational
Laplace transforms. This means the Laplace transform must be of the form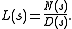
Also, the following conditions must be met.
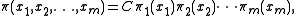
where C is a normalizing constant chosen to make the equilibrium state probabilities sum to 1 and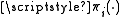 represents the equilibrium distribution for queue i.
represents the equilibrium distribution for queue i.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a discipline within the mathematical theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a BCMP network is a class of queueing network
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
for which a product form equilibrium distribution
Product form solution
In probability theory, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components...
exists. It is named after the authors of the paper where the network was first described: Baskett, Chandy
K. Mani Chandy
Kanianthra Mani Chandy is the Simon Ramo Professor of Computer Science at the California Institute of Technology. He has been the Executive Officer of the Computer Science Department twice, and he has been a professor at Caltech since 1989....
, Muntz and Palacios. The theorem is a significant extension to a Jackson network allowing virtually arbitrary customer routing and service time distributions, subject to particular service disciplines.
The paper is well known, and the theorem was described in 1990 as "one of the seminal achievements in queueing theory in the last 20 years" by J. Michael Harrison
J. Michael Harrison
J. Michael Harrison is an American scientist, known for his contributions to the theory of mathematical finance, in particularstochastic networks and financial engineering. He has authorednear 90 journal articles and written two books in his area....
and Ruth Williams.
Definition of a BCMP network
A network of m interconnected queues is known as a BCMP network if each of the queues is of one of the following four types:- FCFSFirst-come, first-servedFirst-come, first-served – sometimes first-in, first-served and first-come, first choice – is a service policy whereby the requests of customers or clients are attended to in the order that they arrived, without other biases or preferences. The policy can be employed when processing sales orders,...
discipline where all customers have the same negative exponentialExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
service time distribution. The service rate can be state dependent, so write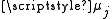 for the service rate when the queue length is j.
for the service rate when the queue length is j. - Processor sharing queues
- Infinite server queues
- LCFS with pre-emptive resume (work is not lost)
In the final three cases, service time distributions must have rational
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
Laplace transforms. This means the Laplace transform must be of the form
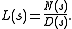
Also, the following conditions must be met.
- external arrivals to node i (if any) form a Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
, - a customer completing service at queue i will either move to some new queue j with (fixed) probability
 or leave the system with probability
or leave the system with probability 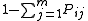 , which is non-zero for some subset of the queues.
, which is non-zero for some subset of the queues.
Theorem
For a BCMP network of m queues which is open, closed or mixed in which each queue is of type 1, 2, 3 or 4, the equilibrium state probabilities are given by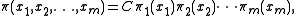
where C is a normalizing constant chosen to make the equilibrium state probabilities sum to 1 and
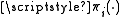 represents the equilibrium distribution for queue i.
represents the equilibrium distribution for queue i.
