Automatic differentiation
Encyclopedia
In mathematics
and computer algebra, automatic differentiation (AD), sometimes alternatively called algorithmic differentiation, is a set of techniques to numerically evaluate the derivative
of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule
repeatedly to these operations, derivatives of arbitrary order can be computed automatically, and accurate to working precision.
Automatic differentiation is not:
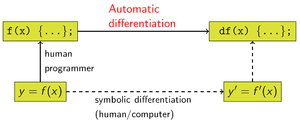
These classical methods run into problems: symbolic differentiation works at low speed, and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off error
s in the discretization
process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient
-based optimization
algorithms. Automatic differentiation solves all of these problems.
. For the simple composition
the chain rule gives
Usually, two distinct modes of AD are presented, forward accumulation (or forward mode) and reverse accumulation (or reverse mode). Forward accumulation specifies that one traverses the chain rule from right to left (that is, first one computes
and then 
), while reverse accumulation has the traversal from left to right.
is interpreted (by a computer or human programmer) as the sequence of elementary operations on the work variables 
, and an AD tool for forward accumulation adds the corresponding operations on the second component of the augmented arithmetic.
The derivative computation for
needs to be seeded in order to distinguish between the derivative with respect to 
or 
. The table above seeds the computation with 
and 
and we see that this results in 
which is the derivative with respect to 
. Note that although the table displays the symbolic derivative, in the computer it is always the evaluated (numeric) value that is stored. Figure 2 represents the above statements in a computational graph.
In order to compute the gradient of this example function, that is
and 
, two sweeps over the computational graph is needed, first with the seeds 
and 
, then with 
and 
.
The computational complexity
of one sweep of forward accumulation is proportional to the complexity of the original code.
Forward accumulation is superior to reverse accumulation for functions
with 
as only one sweep is necessary, compared to 
sweeps for reverse accumulation.
, which may represent a significant memory issue.
The data flow graph of a computation can be manipulated to calculate the gradient of its original calculation. This is done by adding an adjoint node for each primal node, connected by adjoint edges which parallel the primal edges but flow in the opposite direction. The nodes in the adjoint graph represent multiplication by the derivatives of the functions calculated by the nodes in the primal. For instance, addition in the primal causes fanout in the adjoint; fanout in the primal causes addition in the adjoint; a unary function
in the primal causes 
in the adjoint; etc.
Reverse accumulation is superior to forward accumulation for functions
with 
, where forward accumulation requires roughly n times as much work.
Backpropagation
of errors in multilayer perceptrons, a technique used in machine learning, is a special case of reverse mode AD.
of 
is an 
matrix. The Jacobian can be computed using 
sweeps of forward accumulation, of which each sweep can yield a column vector of the Jacobian, or with 
sweeps of reverse accumulation, of which each sweep can yield a row vector of the Jacobian.
with a minimum number of arithmetic operations is known as the "optimal Jacobian accumulation" (OJA) problem. OJA is NP-complete
.
Central to this proof is the idea that there may exist algebraic dependences between the local partials that label the edges of the graph. In particular, two or more edge labels may be recognized as equal. The complexity of the problem is still open if it is assumed that all edge labels are unique and algebraically independent.
of real numbers and obtaining a new arithmetic
. An additional component is added to every number which will represent the derivative of a function at the number, and all arithmetic operators are extended for the augmented algebra. The augmented algebra is the algebra of dual numbers. Computer programs usually implement this using the complex number representation and it is often called the complex-step derivative.
Replace every number
with the number 
, where 
is a real number, but 
is nothing but a symbol with the property 
. Using only this, we get for the regular arithmetic
and likewise for subtraction and division.
Now, we may calculate polynomials in this augmented arithmetic. If
, then
where
denotes the derivative of 
with respect to its first argument, and
, called a seed, can be chosen arbitrarily.
The new arithmetic consists of ordered pair
s, elements written
, with ordinary arithmetics on the first component, and first order differentiation arithmetic on the second component, as described above. Extending the above results on polynomials to analytic functions we obtain a list of the basic arithmetic and some standard functions for the new arithmetic:
and in general for the primitive function
,
where
and 
are the derivatives of 
with respect to its first and second arguments, respectively.
When a binary basic arithmetic operation is applied to mixed arguments — the pair
and the real number 
— the real number is first lifted to 
. The derivative of a function 
at the point 
is now found by calculating 
using the above arithmetic, which gives 
as the result.
of 
at 
in the direction 
by calculating 
using the same arithmetic as above.
arithmetic is used. This is possible because the Taylor summands in a Taylor series of a function are products of known coefficients and derivatives of the function. Computations of Hessian
s using AD has proven useful in some optimization contexts.
The source code for a function is replaced by an automatically generated source code that includes statements for calculating the derivatives interleaved with the original instructions.
Source code transformation can be implemented for all programming languages, and it is also easier for the compiler to do compile time optimizations. However, the implementation of the AD tool itself is more difficult.
Operator overloading
is a possibility for source code written in a language supporting it. Objects for real numbers and elementary mathematical operations must be overloaded to cater for the augmented arithmetic depicted above. This requires no change in the form or sequence of operations in the original source code for the function to be differentiated, but often requires changes in basic data types for numbers and vectors to support overloading and often also involves the insertion of special flagging operations.
Operator overloading for forward accumulation is easy to implement, and also possible for reverse accumulation. However, current compilers lag behind in optimizing the code when compared to forward accumulation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer algebra, automatic differentiation (AD), sometimes alternatively called algorithmic differentiation, is a set of techniques to numerically evaluate the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function specified by a computer program. AD exploits the fact that every computer program, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
repeatedly to these operations, derivatives of arbitrary order can be computed automatically, and accurate to working precision.
Automatic differentiation is not:
- Symbolic differentiation, or
- Numerical differentiationNumerical differentiationIn numerical analysis, numerical differentiation describes algorithms for estimating the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.-Finite difference formulae:...
(the method of finite differences).
These classical methods run into problems: symbolic differentiation works at low speed, and faces the difficulty of converting a computer program into a single expression, while numerical differentiation can introduce round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s in the discretization
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
process and cancellation. Both classical methods have problems with calculating higher derivatives, where the complexity and errors increase. Finally, both classical methods are slow at computing the partial derivatives of a function with respect to many inputs, as is needed for gradient
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
-based optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
algorithms. Automatic differentiation solves all of these problems.
The chain rule, forward and reverse accumulation
Fundamental to AD is the decomposition of differentials provided by the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
. For the simple composition
the chain rule givesUsually, two distinct modes of AD are presented, forward accumulation (or forward mode) and reverse accumulation (or reverse mode). Forward accumulation specifies that one traverses the chain rule from right to left (that is, first one computes
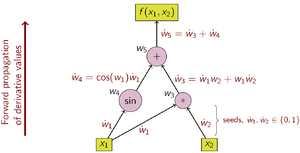
and then ), while reverse accumulation has the traversal from left to right.Forward accumulation
Forward accumulation automatic differentiation is the easiest to understand and to implement. The function is interpreted (by a computer or human programmer) as the sequence of elementary operations on the work variables , and an AD tool for forward accumulation adds the corresponding operations on the second component of the augmented arithmetic.
| Original code statements | Added statements for derivatives |
|---|---|
 |
 (seed) |
 |
 (seed) |
 |
 |
 |
 |
 |
 |
The derivative computation for
needs to be seeded in order to distinguish between the derivative with respect to or . The table above seeds the computation with and and we see that this results in which is the derivative with respect to . Note that although the table displays the symbolic derivative, in the computer it is always the evaluated (numeric) value that is stored. Figure 2 represents the above statements in a computational graph.In order to compute the gradient of this example function, that is
and , two sweeps over the computational graph is needed, first with the seeds and , then with and .The computational complexity
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
of one sweep of forward accumulation is proportional to the complexity of the original code.
Forward accumulation is superior to reverse accumulation for functions
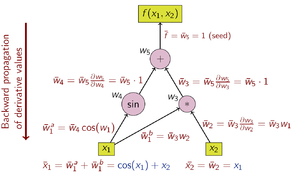
with as only one sweep is necessary, compared to sweeps for reverse accumulation.Reverse accumulation
Reverse accumulation traverses the chain rule from left to right, or in the case of the computational graph in Figure 3, from top to bottom. The example function is real-valued, and thus there is only one seed for the derivative computation, and only one sweep of the computational graph is needed in order to calculate the (two-component) gradient. This is only half the work when compared to forward accumulation, but reverse accumulation requires the storage of some of the work variables, which may represent a significant memory issue.The data flow graph of a computation can be manipulated to calculate the gradient of its original calculation. This is done by adding an adjoint node for each primal node, connected by adjoint edges which parallel the primal edges but flow in the opposite direction. The nodes in the adjoint graph represent multiplication by the derivatives of the functions calculated by the nodes in the primal. For instance, addition in the primal causes fanout in the adjoint; fanout in the primal causes addition in the adjoint; a unary function
in the primal causes in the adjoint; etc.Reverse accumulation is superior to forward accumulation for functions
with , where forward accumulation requires roughly n times as much work.Backpropagation
Backpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
of errors in multilayer perceptrons, a technique used in machine learning, is a special case of reverse mode AD.
Jacobian computation
The JacobianJacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of is an matrix. The Jacobian can be computed using sweeps of forward accumulation, of which each sweep can yield a column vector of the Jacobian, or with sweeps of reverse accumulation, of which each sweep can yield a row vector of the Jacobian.Beyond forward and reverse accumulation
Forward and reverse accumulation are just two (extreme) ways of traversing the chain rule. The problem of computing a full Jacobian of with a minimum number of arithmetic operations is known as the "optimal Jacobian accumulation" (OJA) problem. OJA is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
Central to this proof is the idea that there may exist algebraic dependences between the local partials that label the edges of the graph. In particular, two or more edge labels may be recognized as equal. The complexity of the problem is still open if it is assumed that all edge labels are unique and algebraically independent.
Automatic differentiation using dual numbers
Forward mode automatic differentiation is accomplished by augmenting the algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of real numbers and obtaining a new arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. An additional component is added to every number which will represent the derivative of a function at the number, and all arithmetic operators are extended for the augmented algebra. The augmented algebra is the algebra of dual numbers. Computer programs usually implement this using the complex number representation and it is often called the complex-step derivative.
Replace every number
with the number , where is a real number, but is nothing but a symbol with the property . Using only this, we get for the regular arithmeticand likewise for subtraction and division.
Now, we may calculate polynomials in this augmented arithmetic. If
, then |
 |
 |
 |
 |
|
 |
||
 |
 |
where
denotes the derivative of with respect to its first argument, and, called a seed, can be chosen arbitrarily.The new arithmetic consists of ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s, elements written
, with ordinary arithmetics on the first component, and first order differentiation arithmetic on the second component, as described above. Extending the above results on polynomials to analytic functions we obtain a list of the basic arithmetic and some standard functions for the new arithmetic:and in general for the primitive function
,where
and are the derivatives of with respect to its first and second arguments, respectively.When a binary basic arithmetic operation is applied to mixed arguments — the pair
and the real number — the real number is first lifted to . The derivative of a function at the point is now found by calculating using the above arithmetic, which gives as the result.Vector arguments and functions
Multivariate functions can be handled with the same efficiency and mechanisms as univariate functions by adopting a directional derivative operator, which finds the directional derivative of at in the direction by calculating using the same arithmetic as above.Higher order differentials
The above arithmetic can be generalized, in the natural way, to second order and higher derivatives. However, the arithmetic rules quickly grow very complicated: complexity will be quadratic in the highest derivative degree. Instead, truncated Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
arithmetic is used. This is possible because the Taylor summands in a Taylor series of a function are products of known coefficients and derivatives of the function. Computations of Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
s using AD has proven useful in some optimization contexts.
Implementation
Forward-mode AD is implemented by a Nonstandard interpretation of the program in which real numbers are replaced by dual numbers, constants are lifted to dual numbers with a zero epsilon coefficient, and the numeric primitives are lifted to operate on dual numbers. This nonstandard interpretation is generally implemented using one of two strategies: source code transformation or operator overloading.Source code transformation
Source code transformation can be implemented for all programming languages, and it is also easier for the compiler to do compile time optimizations. However, the implementation of the AD tool itself is more difficult.
Operator overloading
Operator overloading
In object oriented computer programming, operator overloading—less commonly known as operator ad-hoc polymorphism—is a specific case of polymorphism, where different operators have different implementations depending on their arguments...
is a possibility for source code written in a language supporting it. Objects for real numbers and elementary mathematical operations must be overloaded to cater for the augmented arithmetic depicted above. This requires no change in the form or sequence of operations in the original source code for the function to be differentiated, but often requires changes in basic data types for numbers and vectors to support overloading and often also involves the insertion of special flagging operations.
Operator overloading for forward accumulation is easy to implement, and also possible for reverse accumulation. However, current compilers lag behind in optimizing the code when compared to forward accumulation.
Software
- C/C++
Package License Approach Brief Info ADC Version 4.0 nonfree OO ADIC free for noncommercial SCT forward mode ADMB ADMBADMB or AD Model Builder is a free and open source software suite for non-linear statistical modeling. It was created by David Fournier and now being developed by the ADMB Project, a creation of the non-profit ADMB Foundation...OO ADOL-C CPL 1.0 or GPL 2.0 OO now a part of COIN-OR COIN-ORCOIN-OR, which stands for Computational Infrastructure for Operations Research, is a project that aims to "create for mathematical software what the open literature is for mathematical theory." The open literature provides the OR community with a peer-review process and an archive...
projectAMPL AMPLAMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and solving high-complexity problems for large-scale mathematical computation AMPL, an acronym for "A Mathematical Programming Language", is an algebraic modeling language for describing and...free for students SCT FADBAD++ free for
noncommercialOO uses operator new CasADi LGPL OO/SCT Forward/reverse modes, matrix-valued atomic operations. CppAD CPL 1.0 or GPL 2.0 OO a part of COIN-OR project OpenAD depends on components SCT Sacado OO A part of the Trilinos collection, forward/reverse modes. TAPENADE Free for noncommercial SCT CTaylor not free OO truncated taylor series, multi variable, high performance, calculating and storing only potentially nonzero derivatives, calculates higher order derivatives, order of derivatives increases when using matching operations until maximum order (parameter) is reached, example source code and executable available for testing performance
- Fortran
Package License Approach Brief Info ADF Version 4.0 nonfree OO ADIFOR >>>
(free for non-commercial)SCT AUTO_DERIV free for non-commercial OO OpenAD depends on components SCT TAPENADE Free for noncommercial SCT
- Matlab
Package License Approach Brief Info AD for MATLAB OO Forward (1st & 2nd derivative, Uses MEX files & Windows DLLs) Adiff OO Forward (1st derivative) MAD Proprietary OO ADiMat ? SCT Forward (1st & 2nd derivative) & Reverse (1st) myAD OO Forward (1st & 2nd derivative)
- Python
Package License Approach Brief Info FuncDesigner FuncDesignerFuncDesigner is a computer algebra system written as a Python module. It is cross-platform software , with a completely free license....OO uses NumPy arrays and SciPy SciPySciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
sparse matrices,
also allows to solve linear/non-linear/ODE systems and
to perform numerical optimizations by OpenOptOpenOptOpenOpt is an open-source framework for numerical optimization, nonlinear equations and systems of them. It is licensed under the BSD license, making it available to be used in both open- and closed-code software. The package already has some essential ....ScientificPython CeCILL CeCILLCeCILL is a free software license adapted to both international and French legal matters, in the spirit of and retaining compatibility with the GNU General Public License....OO see modules Scientific.Functions.FirstDerivatives and
Scientific.Functions.Derivativespycppad OO wrapper for CppAD, second order forward/reverse pyadolc OO wrapper for ADOL-C, hence arbitrary order derivatives in the (combined) forward/reverse mode of AD, supports sparsity pattern propagation and sparse derivative computations uncertainties OO first-order derivatives, reverse mode, transparent calculations algopy OO same approach as pyadolc and thus compatible, support to differentiate through numerical linear algebra functions like the matrix-matrix product, solution of linear systems, QR and Cholesky decomposition, etc. pyderiv OO automatic differentiation and (co)variance calculation CasADi LGPL OO/SCT Python front-end to CasADi. Forward/reverse modes, matrix-valued atomic operations.
- C#
Package License Approach Brief Info AutoDiff OO Automatic differentiation with C# operators overloading. FuncLib MIT MIT LicenseThe MIT License is a free software license originating at the Massachusetts Institute of Technology . It is a permissive license, meaning that it permits reuse within proprietary software provided all copies of the licensed software include a copy of the MIT License terms...OO Automatic differentiation and numerical optimization, operator overloading, unlimited order of differentiation, compilation to IL code for very fast evaluation.
- Haskell
Package License Approach Brief Info ad OO Forward Mode (1st derivative or arbitrary order derivatives via lazy lists and sparse tries)
Reverse Mode
Combined forward-on-reverse Hessians.
Uses Quantification to allow the implementation automatically choose appropriate modes.
Quantification prevents perturbation/sensitivity confusion at compile time.fad OO Forward Mode (lazy list). Quantification prevents perturbation confusion at compile time. rad OO Reverse Mode. (Subsumed by 'ad').
Quantification prevents sensitivity confusion at compile time.
- Octave
Package License Approach Brief Info CasADi LGPL OO/SCT Octave front-end to CasADi. Forward/reverse modes, matrix-valued atomic operations.
External links
- www.autodiff.org, An "entry site to everything you want to know about automatic differentiation"
- Automatic Differentiation of Parallel OpenMP Programs
- Automatic Differentiation, C++ Templates and Photogrammetry
- Automatic Differentiation, Operator Overloading Approach
- Compute analytic derivatives of any Fortran77, Fortran95, or C program through a web-based interface Automatic Differentiation of Fortran programs
- Description and example code for forward Automatic Differentiation in Scala