Asymptotic theory (statistics) - AbsoluteAstronomy.com

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, asymptotic theory, or large sample theory, is a generic framework for assessment of properties of estimator

Estimator

In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....

s and statistical tests. Within this framework it is typically assumed that the sample size

Sample size

Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...

n grows indefinitely, and the properties of statistical procedures are evaluated in the limit as .

In practical applications, asymptotic theory is applied by treating the asymptotic results as approximately valid for finite sample sizes as well. Such approach is often criticized for not having any mathematical grounds behind it, yet it is used ubiquitously anyway. The importance of the asymptotic theory is that it often makes possible to carry out the analysis and state many results which cannot be obtained within the standard “finite-sample theory”.

Overview

Most statistical problems begin with a dataset of size

Sample size

n. The asymptotic theory proceeds by assuming that it is possible to keep collecting additional data, so that the sample size would grow indefinitely:

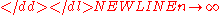
Under this assumption many results can be obtained that are unavailable for samples of finite sizes. As an example consider the law of large numbers

Law of large numbers

In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...

. This law states that for a sequence of iid random variables X₁, X₂, …, the sample averages

\scriptstyle\overline{X}_n

converge in probability to the population mean E[X_i] as n → ∞. At the same time for finite n it is impossible to claim anything about the distribution of

\scriptstyle\overline{X}_n

if the distributions of individual X_i’s is unknown.

For various models slightly different modes of asymptotics may be used:

For cross-sectional data
Cross-sectional data
Cross-sectional data or cross section in statistics and econometrics is a type of one-dimensional data set. Cross-sectional data refers to data collected by observing many subjects at the same point of time, or without regard to differences in time...

(iid) the new observations are sampled independently, from the same fixed distribution. This is the standard case of asymptotics.
For longitudinal data (time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...

) the sampling method may differ from model to model. Sometimes the data is assumed to be ergodic
Ergodic process
In signal processing, a stochastic process is said to be ergodic if its statistical properties can be deduced from a single, sufficiently long sample of the process.- Specific definitions :...

, in other applications it can be integrated or cointegrated
Cointegration
Cointegration is a statistical property of time series variables. Two or more time series are cointegrated if they share a common stochastic drift.-Introduction:...

. In this case the asymptotic is again taken as the number of observations (usually denoted T in this case) goes to infinity: .
For panel data
Panel data
In statistics and econometrics, the term panel data refers to multi-dimensional data. Panel data contains observations on multiple phenomena observed over multiple time periods for the same firms or individuals....

, it is commonly assumed that one dimension in the data (T) remains fixed, whereas the other dimension grows: , .

Besides these standard approaches, various other “alternative” asymptotic approaches exist:

Within the local asymptotic normality
Local asymptotic normality
In statistics, local asymptotic normality is a property of a sequence of statistical models, which allows this sequence to be asymptotically approximated by a normal location model, after a rescaling of the parameter...

framework, it is assumed that the value of the “true parameter” in the model varies slightly with n, such that the n-th model corresponds to $\scriptstyle\theta_n\,=\,\theta+h/\sqrt{n}$ . This approach lets us study the regularity of estimators.
When statistical tests are studied for their power to distinguish against the alternatives that are close to the null hypothesis, it is done within the so-called “local alternatives” framework: the null hypothesis is H₀: θ = θ₀, and the alternative is H₁: $\scriptstyle\theta\,=\,\theta_0+h/\sqrt{n}$ . This approach is especially popular for the unit root test
Unit root test
In statistics, a unit root test tests whether a time series variable is non-stationary using an autoregressive model. A well-known test that is valid in large samples is the augmented Dickey–Fuller test. The optimal finite sample tests for a unit root in autoregressive models were developed by John...

s.
There are models where the dimension of the parameter space Θ_n slowly expands with n, reflecting the fact that the more observations a statistician has, the more he is tempted to introduce additional parameters in the model. An example of this is the weak instruments asymptotic.
In kernel density estimation
Kernel density estimation
In statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...

and kernel regression
Kernel regression
The kernel regression is a non-parametric technique in statistics to estimate the conditional expectation of a random variable. The objective is to find a non-linear relation between a pair of random variables X and Y....

additional parameter — the bandwidth h — is assumed. In these models it is typically taken that h → 0 as n → ∞, however the rate of convergence must be chosen carefully, usually h ∝ n^−1/5.

Estimators

Consistency
Consistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

: a sequence of estimators is said to be consistent, if it converges in probability to the true value of the parameter being estimated:

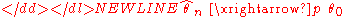
Generally an estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....

is just some, more or less arbitrary, function of the data. The property of consistency requires that the estimator was estimating the quantity we intended it to. As such, it is the most important property in the estimation theory: estimators that are known to be inconsistent are never used in practice.

Asymptotic distribution
Asymptotic distribution
In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...

: if it is possible to find sequences of non-random constants {a_n}, {b_n} (possibly depending on the value of θ₀), and a non-degenerate distribution G such that

then the sequence of estimators $\scriptstyle\hat\theta_n$ is said to have the asymptotic distribution G.

Most often, the estimators encountered in practice have the asymptotically normal distribution, with , , and :

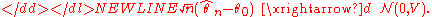
Asymptotic confidence region
Confidence region
In statistics, a confidence region is a multi-dimensional generalization of a confidence interval. It is a set of points in an n-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur.The confidence region is...

s.

Regularity.

Asymptotic theorems

Law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
Central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
Slutsky’s theorem
Continuous mapping theorem
Continuous mapping theorem
In probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.