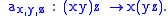Associator
Encyclopedia
In abstract algebra
, the term associator is used in different ways as a measure of the nonassociativity
of an algebraic structure.
or algebra
, the associator is the multilinear map 
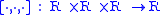given by
Just as the commutator
measures the degree of noncommutativity
, the associator measures the degree of nonassociativity of
.
It is identically zero for an associative ring or algebra.
The associator in any ring obeys the identity
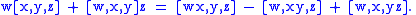
The associator is alternating precisely when
is an alternative ring.
The associator is symmetric in its two rightmost arguments when
is a pre-Lie algebra
.
Q is a set with a binary operation
such that for each a,b in Q,
the equations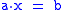
and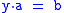 
have unique solutions x,y in Q. In a quasigroup Q, the
associator is the map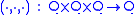
defined by the equation
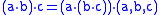
for all a,b,c in Q. As with its ring theory analog, the quasigroup associator is a measure of nonassociativity of Q.
, where there may be non-identity morphisms between algebraic expressions, an associator is an isomorphism
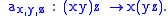
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the term associator is used in different ways as a measure of the nonassociativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of an algebraic structure.
Ring theory
For a nonassociative ringNonassociative ring
In abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
or algebra
, the associator is the multilinear map 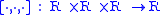given byJust as the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
measures the degree of noncommutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, the associator measures the degree of nonassociativity of
.It is identically zero for an associative ring or algebra.
The associator in any ring obeys the identity
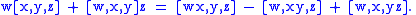
The associator is alternating precisely when
is an alternative ring.The associator is symmetric in its two rightmost arguments when
is a pre-Lie algebraPre-Lie algebra
In mathematics, a pre-Lie algebra is an algebraic structure on a vector space, that describes some properties of objects such as rooted trees and vector fields on affine space....
.
Quasigroup theory
A quasigroupQuasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
Q is a set with a binary operation
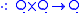such that for each a,b in Q,the equations
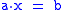and 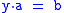have unique solutions x,y in Q. In a quasigroup Q, theassociator is the map
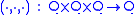defined by the equation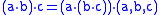for all a,b,c in Q. As with its ring theory analog, the quasigroup associator is a measure of nonassociativity of Q.
Higher-dimensional algebra
In higher-dimensional algebraHigher-dimensional algebra
Supercategories were first introduced in 1970, and were subsequently developed for applications in theoretical physics and mathematical biology or mathematical biophysics....
, where there may be non-identity morphisms between algebraic expressions, an associator is an isomorphism