
Askey–Wilson polynomials
Encyclopedia
In mathematics, the Askey–Wilson polynomials (or q-Wilson polynomials) are a family of orthogonal polynomials
introduced by as q-analog
s of the Wilson polynomials
. They include many of the other orthogonal polynomials in 1 variable as special or limiting cases, described in the Askey scheme
. Askey–Wilson polynomials are the special case of Macdonald polynomials (or Koornwinder polynomials
) for the non-reduced affine root system
of type (C, C1), and their 4 parameters a, b, c, d correspond to the 4 orbits of roots of this root system.
They are defined by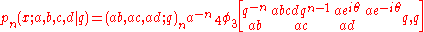
where φ is a basic hypergeometric function and x = cos(θ) and n is the q-Pochhammer symbol. Askey–Wilson functions are a generalization to non-integral values of n.
Askey–Wilson polynomials are the special case of Koornwinder polynomials
(or Macdonald polynomials) for the non-reduced root system of type (C, C1).
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
introduced by as q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
s of the Wilson polynomials
Wilson polynomials
In mathematics, Wilson polynomials are a family of orthogonal polynomials introduced by that generalize Jacobi polynomials, Hahn polynomials, and Charlier polynomials....
. They include many of the other orthogonal polynomials in 1 variable as special or limiting cases, described in the Askey scheme
Askey scheme
In mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in , the Askey scheme was first drawn by and by , and has since been extended by and to cover basic...
. Askey–Wilson polynomials are the special case of Macdonald polynomials (or Koornwinder polynomials
Koornwinder polynomials
In mathematics, Koornwinder polynomials are a family of orthogonal polynomials in several variables, introduced by , that generalize the Askey-Wilson polynomials...
) for the non-reduced affine root system
Affine root system
In mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root...
of type (C, C1), and their 4 parameters a, b, c, d correspond to the 4 orbits of roots of this root system.
They are defined by
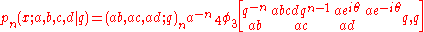
where φ is a basic hypergeometric function and x = cos(θ) and n is the q-Pochhammer symbol. Askey–Wilson functions are a generalization to non-integral values of n.
Askey–Wilson polynomials are the special case of Koornwinder polynomials
Koornwinder polynomials
In mathematics, Koornwinder polynomials are a family of orthogonal polynomials in several variables, introduced by , that generalize the Askey-Wilson polynomials...
(or Macdonald polynomials) for the non-reduced root system of type (C, C1).

