Wilson polynomials
Encyclopedia
In mathematics, Wilson polynomials are a family of orthogonal polynomials
introduced by
that generalize Jacobi polynomials
, Hahn polynomials
, and Charlier polynomials
.
They are defined in terms of the generalized hypergeometric function and the Pochhammer symbol
s by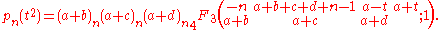
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
introduced by
that generalize Jacobi polynomials
Jacobi polynomials
In mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
, Hahn polynomials
Hahn polynomials
In mathematics, the Hahn polynomials are a family of orthogonal polynomials in the Askey scheme of hypergeometric orthogonal polynomials, introduced by Chebyshev in 1875 and rediscovered by . The Hahn class is a name for special cases of Hahn polynomials, including Hahn polynomials, Meixner...
, and Charlier polynomials
Charlier polynomials
In mathematics, Charlier polynomials are a family of orthogonal polynomials introduced by Carl Charlier....
.
They are defined in terms of the generalized hypergeometric function and the Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
s by