
Ars Conjectandi
Encyclopedia

Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
paper written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli
Nicolaus I Bernoulli
Nicolaus Bernoulli , was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family....
. The seminal work consolidated, most notably among other combinatorial topics, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
: indeed, it is widely regarded as the founding work of that subject. It also addressed problems that today are classified in the twelvefold way
Twelvefold way
In combinatorics, the twelvefold way is a name given to a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number...
, and added to the subjects; consequently, it has been dubbed an important historical landmark in not only probability but all combinatorics by a plethora of mathematical historians. The importance of this early work had a large impact on both contemporary and later mathematicians; for example, Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
.
Bernoulli wrote the text between 1684 and 1689, including the work of mathematicians such as Christian Huygens, Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
, Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, and Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
. He incorporated fundamental combinatorial topics such as his theory of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s and combination
Combination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
s—the aforementioned problems from the twelvefoldway—as well as those more distantly connected to the burgeoning subject: the derivation and properties of the eponymous Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s, for instance. Core topics from probability, such as expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, were also a significant portion of this important work.
Background

Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
was first formally developed in the sixteenth century with the work of Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
, whose interest in the branch of mathematics was largely due to his habit of gambling. He formalized what is now called the classical definition of probability: if an event has a possible outcomes and we select any b of those such that b ≤ a, the probability of any of the b occurring is
 . However, his actual influence on mathematical scene was not great; he wrote only one light tome on the subject in 1525 titled Liber de ludo aleae (Book on Games of Chance), which was published posthumously in 1663.
. However, his actual influence on mathematical scene was not great; he wrote only one light tome on the subject in 1525 titled Liber de ludo aleae (Book on Games of Chance), which was published posthumously in 1663.The date which historians cite as the beginning of the development of modern probability theory is 1654, when two of the most well-known mathematicians of the time, Blaise Pascal and Pierre de Fermat, began a correspondence discussing the subject. The two initiated the communication because earlier that year, a gambler from Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
named Antoine Gombaud
Antoine Gombaud
Antoine Gombaud, Chevalier de Méré was a French writer, born at Poitou in 1607, and died on December 29, 1684. Although he was not a nobleman, he adopted the title Chevalier for the character in his dialogues who represented his own views...
had sent Pascal and other mathematicians several questions on the practical applications of some of these theories; in particular he posed the problem of points
Problem of points
The problem of points, also called the problem of division of the stakes, is a classical problem in probability theory. One of the famous problems that motivated the beginnings of modern probability theory in the 17th century, it led Blaise Pascal to the first explicit reasoning about what today is...
, concerning a theoretical two-player game in which a prize must be divided between the players due to external circumstances halting the game. The fruits of Pascal and Fermat's correspondence interested other mathematicians, including Christian Huygens, who in 1657 published De ratiociniis in aleae ludo (Calculations in Games of Chance). During this period, Pascal also published his results on the eponymous Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, an important combinatorial concept. He referred to the triangle in his work Traité du triangle arithmétique (Traits of the Arithmetic Triangle) as the "arithmetic triangle". Later, Johan de Witt
Johan de Witt
Johan de Witt, heer van Zuid- en Noord-Linschoten, Snelrewaard, Hekendorp and IJsselveere was a key figure in Dutch politics in the mid 17th century, when its flourishing sea trade in a period of globalization made the United Provinces a leading European power during the Dutch Golden Age...
published similar material in his 1671 work Waerdye van Lyf-Renten (A Treatise on Life Annuities), which used statistical concepts to determine life expectancy
Life expectancy
Life expectancy is the expected number of years of life remaining at a given age. It is denoted by ex, which means the average number of subsequent years of life for someone now aged x, according to a particular mortality experience...
for practical political purposes; a demonstration of the fact that this sapling branch of mathematics had significant pragmatic applications.
In the wake of all this pioneers, Bernoulli produced Ars Conjectandi, during a fertile mathematical period he had between 1684 and 1689. When he began the work in 1684 at the age of 30, while intrigued by combinatorial and probabilistic problems, Bernoulli had not yet read Pascal's work on the "arithmetic triangle" nor de Witt's work on the applications of probability theory: he had earlier requested a copy of the latter from his acquaintance Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
, but Leibniz failed to provide it. The latter, however, did manage to provide Pascal's and Huygen's work, and thus it is largely upon these foundations that Ars Conjectandi is constructed. From the outset, Bernoulli wished for his work to demonstrate that combinatorial and probability theory would have numerous real-world applications in all facets of society—in the line of de Witt's work—and thus the title Ars Conjectandi was chosen: a link to the concept of ars inveniendi
Ars inveniendi
Ars inveniendi is a chief notion of mathesis universalis and implies ascertaining truth through the use of mathematics....
from scholasticism
Scholasticism
Scholasticism is a method of critical thought which dominated teaching by the academics of medieval universities in Europe from about 1100–1500, and a program of employing that method in articulating and defending orthodoxy in an increasingly pluralistic context...
, which provided the symbolic link to pragmatism he desired. His nephew Niklaus published the manuscript in 1713 after Bernoulli's death in 1705.
Contents

Twelvefold way
In combinatorics, the twelvefold way is a name given to a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number...
. It also discusses the motivation and applications of a sequence of numbers more closely related to number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
than probability; these Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s bear his name today, and are one of his more notable achievements.
The first part is an in-depth expository on Huygens' De ratiociniis in aleae ludo. Bernoulli provides in this section solutions to the problems Huygens posed at the end of his work. He particularly develops Huygens' concept of expected value—the weighted average of all possible outcomes of an event. Huygens had developed the following formula:
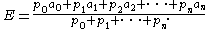
In this formula, E is the expected value, pi are the probabilities of attaining each value, and ai are the attainable values. Bernoulli normalizes the expected value by assuming that pi are the probabilities of all the disjoint outcomes of the value, hence implying that p0 + p1 + ... + pn = 1. Another key theory developed in this part is the probability of achieving at least a certain number of successes from a number of binary events, today named Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
s, given that the probability of success in each event was the same. Bernoulli shows through mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
that given a the number of favorable outcomes in each event, b the number of total outcomes in each event, d the desired number of successful outcomes, and e the number of events, the probability of at least d successes is
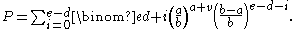
The first part concludes with what is now known as the Bernoulli distribution.
The second part expands on enumerative combinatorics, or the systematic numeration of objects. It was in this part that two of the most important of the twelvefold ways—the permutations and combinations that would form the basis of the subject—were fleshed out, though they had been introduced earlier for the purposes of probability theory. On a note more distantly related to combinatorics, the second section also discusses the general formula for sums of integer powers; the free coefficients of this formula are therefore called the Bernoulli numbers, which have proven to have numerous applications in number theory. Additionally, this part also contains Bernoulli's formula for the sum of powers of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, which influenced Abraham de Moivre's work later.
In the third part, Bernoulli applies the probability techniques from the first section to the common chance games played with playing cards or dice. He presents probability problems related to these and, once a method had been established, posed generalizations. For example, a problem involving the expected number of "court cards"—jack, queen, and king—one would pick in a five-card hand from a standard deck of 52 cards containing 12 court cards could be generalized to a deck with a cards that contained b court cards, and a c-card hand.
The fourth section continues the trend of practical applications by discussing applications of probability to civilibus, moralibus, and oeconomicis, or to personal, judicial, and financial decisions. In this section, Bernoulli differs from the school of thought known as frequentism
Frequency probability
Frequency probability is the interpretation of probability that defines an event's probability as the limit of its relative frequency in a large number of trials. The development of the frequentist account was motivated by the problems and paradoxes of the previously dominant viewpoint, the...
, which defined probability in an empirical sense. As a counter, he produces a result resembling the law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, which he describes as predicting that the results of observation would approach theoretical probability as more trials were held—in contrast, frequents defined probability in terms of the former. Bernoulli was very proud of this result, referring to it as his "golden theorem", and remarked that it was "a problem in which I’ve engaged
myself for twenty years". This early version of the law is known today as either Bernoulli's theorem or the weak law of large numbers, as it is less rigorous and general than the modern version.
After these four primary expository sections, almost as an afterthought, Bernoulli appended to Ars Conjectandi a tract on calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, which concerned infinite series. It was a reprint of five dissertations he had published between 1686 and 1704.
Legacy

Elsevier
Elsevier is a publishing company which publishes medical and scientific literature. It is a part of the Reed Elsevier group. Based in Amsterdam, the company has operations in the United Kingdom, USA and elsewhere....
and edited by historian Ivor Grattan-Guinness
Ivor Grattan-Guinness
Ivor Grattan-Guinness, born 23 June 1941, in Bakewell, in England, is a historian of mathematics and logic.He gained his Bachelor degree as a Mathematics Scholar at Wadham College, Oxford, got an M.Sc in Mathematical Logic and the Philosophy of Science at the London School of Economics in 1966...
describes the studies set out in the work "[occupying] mathematicians throughout 18th and 19th centuries"—an influence lasting three centuries. Statistician Anthony Edwards
A. W. F. Edwards
Anthony William Fairbank Edwards is a British statistician, geneticist, and evolutionary biologist, sometimes called Fisher's Edwards. He is a Life Fellow of Gonville and Caius College and retired Professor of Biometry at the University of Cambridge, and holds both the ScD and LittD degrees. A...
praised not only the book's groundbreaking content, writing that it demonstrated Bernoulli's "thorough familiarity with the many facets [of combinatorics]," but its form: "[Ars Conjectandi] is a very well-written book, excellently constructed." Perhaps most recently, notable popular mathematical historian and topologist William Dunham called the paper "the next milestone of probability theory [after the work of Cardano]" as well as "Jakob Bernoulli's masterpiece". It greatly aided what Dunham describes as "Bernoulli's long-established reputation".
Bernoulli's work influenced many contemporary and subsequent mathematicians. Even the afterthought-like tract on calculus has been quoted frequently; most notably by the Scottish mathematician Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
. Abraham de Moivre was particularly influenced by Bernoulli's work in probability; he wrote extensively on the subject in The Doctrine of Chances
The Doctrine of Chances
The Doctrine of Chances was the first textbook on probability theory, written by 18th-century French mathematician Abraham de Moivre and first published in 1718. De Moivre wrote in English because he resided in England at the time, having fled France to escape the persecution of Huguenots...
. De Moivre's most notable achievement in probability was the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, by which he was able to approximate the binomial distribution, using an asymptotic
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
sequence for the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function—which he had developed with James Stirling
James Stirling (mathematician)
James Stirling was a Scottish mathematician. The Stirling numbers and Stirling's approximation are named after him.-Biography:...
—and Bernoulli's formula for the sum of powers of numbers.
A significant indirect influence was Thomas Simpson
Thomas Simpson
Thomas Simpson FRS was a British mathematician, inventor and eponym of Simpson's rule to approximate definite integrals...
, who achieved a result that closely resembled de Moivre's. According to Simpsons' work's preface, his own work depended greatly on de Moivre's; the latter in fact described Simpson's work as an abridged version of his own. Finally, Thomas Bayes
Thomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
wrote an essay discussing theological
Theology
Theology is the systematic and rational study of religion and its influences and of the nature of religious truths, or the learned profession acquired by completing specialized training in religious studies, usually at a university or school of divinity or seminary.-Definition:Augustine of Hippo...
implications of de Moivre's results: his solution to a problem, namely that of determining the probability of an event by its relative frequency, was taken as a proof for the existence of God
Existence of God
Arguments for and against the existence of God have been proposed by philosophers, theologians, scientists, and others. In philosophical terms, arguments for and against the existence of God involve primarily the sub-disciplines of epistemology and ontology , but also of the theory of value, since...
by Bayes. Indeed, in light of all this, there is good reason Bernoulli's work is hailed as such a seminal event; not only did his various influences, direct and indirect, set the mathematical study of combinatorics spinning, but even theology was impacted.

