
Argus distribution
Encyclopedia
In physics
, the ARGUS distribution, named after the particle physics
experiment ARGUS
, is the probability distribution
of the reconstructed invariant mass of a decayed particle candidate in continuum background.
of the ARGUS distribution is:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the ARGUS distribution, named after the particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
experiment ARGUS
ARGUS (experiment)
The ARGUS experiment was a particle physics experiment that ran at the electron-positron collider ring DORIS II at DESY. It is the first experiment that observed the mixing of the B mesons ....
, is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the reconstructed invariant mass of a decayed particle candidate in continuum background.
Definition
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the ARGUS distribution is:
-
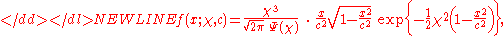
for . Here χ, and c are parameters of the distribution and
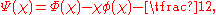
and Φ(·), ϕ(·) are the cumulative distributionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
and probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s of the standard normal distribution, respectively.
Cumulative distribution function
The cdfCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the ARGUS distribution is-

Parameter estimation
Parameter c is assumed to be known (the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
), whereas χ can be estimated from the sample X1, …, Xn using the maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
approach. The estimator is a function of sample second moment, and is given as a solution to the non-linear equation-

The solution exists and is unique, provided that the right-hand side is greater than 0.4; the resulting estimator is consistentConsistent estimatorIn statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
and asymptotically normal.
Generalized ARGUS distribution
Sometimes a more general form is used to describe a more peaking-like distribution:
-

where Γ(·) is the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, and Γ(·,·) is the upper incomplete gamma function.
Here parameters c, χ, p represent the cutoff, curvature, and power respectively.
mode =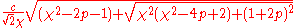
p = 0.5 gives a regular ARGUS, listed above.
Further reading
-
-
-

